Nyquist plot, damping factor and phase margin

[jegues]

Homework Statement

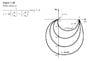
A Nyquist (polar) plot of a standard second-order system is shown below (drawn to scale).

Suppose a unit-step function is applied as the input to this system. Determine the peak percentage overshoot expected in the system output.

Homework Equations

The Attempt at a Solution

My idea was to trace backwards from the ω→+∞ at the origin until I reach a vector from the origin to a point on the curve with magnitude one. This ω will correspond to a gain cross over frequency and provide me with the phase margin.

I could then link this value of the phase margin back to zeta through the following equation,

$$\text{P.M.} = \gamma = tan^{-1}\left( \frac{2\zeta}{\sqrt{-2\zeta^{2}+\sqrt{1+4\zeta^{2}}}}\right)}$$

The first point I could find that would give me a vector of magnitude one resides at (0.6, -0.8) yielding a phase margin of 126.87°. Unfortunately this PM yields a negative value for zeta.

Any idea where I went wrong or an easier way to solve the problem?

 

[jegues]

Bump, still looking for help!

 

[AlephZero]

It might help if you defined what your textbook calls a "standard" 2nd order system.

Looking carefully at the plot, it doesn't go exactly through (0.6, -0.8), but it does go exactly through (1, 0), (0, 0) and (0, -0.8), and the slope at (1,0) is vertical. Is that enough data to fix the transfer function, for your "standard" system?

 

[jegues]

It might help if you defined what your textbook calls a "standard" 2nd order system.

A standard 2nd order system would be in the form,

$$G(s) = \frac{\omega_{n}^{2}}{s^{2}+2\zeta \omega_{n} s + \omega_{n}^2}$$

Looking carefully at the plot, it doesn't go exactly through (0.6, -0.8), but it does go exactly through (1, 0), (0, 0) and (0, -0.8), and the slope at (1,0) is vertical. Is that enough data to fix the transfer function, for your "standard" system?

The only information I can extract out of those three points is that,

$$G(j\omega_{n}) = \frac{1}{j2 \zeta} = -j0.8$$

$$|G(j\omega_{n}| = \frac{1}{2 \zeta} = 0.8$$

$$\Rightarrow \zeta = 0.625$$

So,

$$\text{OS%} = 100 e^{\frac{-\pi \zeta}{\sqrt{1 - \zeta^{2}}}} = 8.083 \text{%}$$

Does the slope at the point (1,0) somehow link back to ζ as well?

 

[rude man]

The problem I have with this is that you speak of a standard 2nd order transfer function, which is well defined: F(s) = (1/(s² + 2ζw_ns + w_n²), which I assume is the closed-loop transfer function.

However, a Nyquist plot is that of the open loop, not the closed loop, and the open loop is not unique to the closed loop.

One candidate however is F(s) = G/(1+G) which is G/(1+GH) with H=1 (unity fedback).

The closed loop is also written as F(s) = 1/(s+s₁)(s+s₂) where s1 and s2 are complex-conjugate pole pairs:
s₁ = a +jb
s₂ = a -jb
where a and b are functions of ζ and w_n.

Solve for G(a,b) from G/(1+G) = 1/(s+a+jb)(s+a-jb) with s = jw.

You can now generate a "template" Nyquist plot of G(jw) with unknown a and b. Then pick values for a and b so as to generate your given plot. This may not be as bad as it seems if you pick your w point judiciously. Knowing a and b you can find w_n and ζ . Finally you have the entire closed loop transfer function and can input a step function and solve for the overshoot.

This seems a really horrible problem that way, there is probably a short-cut of some kind equating open-loop Nyquist plots with the corresponding closed-loop transfer functions, but I don't know it. I'll try to research this a bit further.