Nyquist Sampling Theorem - I just understand this.

[Brad1983]

Hello! I am having a difficult time understanding the "Nyquist Sampling Theorem." I was wondering if someone can help me understand this. Below is an example out of my book:

Q: Suppose that an analog signal is given as
x(t) = 5cos(2*pi*1000t), for t > 0
and is sampled at the rate of 8000 HZ

a.) Sketch the spectrum for the original signal.

A:
They do the Euler Identity:
5cos(2*pi*1000t = (e^{j*2*pi*1000*t} + e^{-j*2*pi*1000*t}) / 2
5cos(2*pi*1000t)= 2.5*e^{j*2*pi*1000*t} + 2.5*e^{-j*2*pi*1000*t}

The coefficient is c1 = 2.5 and c2 = 2.5 and they get the following graph:

--------------------------------------------

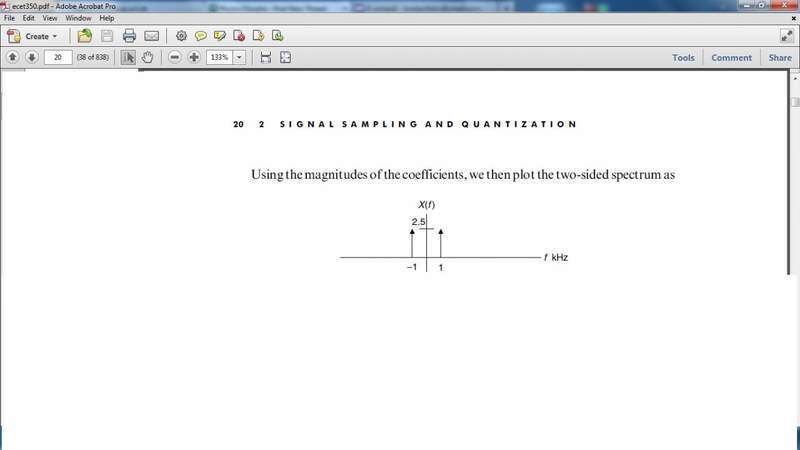
According to what's in my book and my course shell, I am trying to do the example problem like it is in my course shell which is something like this:
I know f_s > 2* f_maxx(t) = 5cos(2*pi*1000t)
f_s = (1 / T_s)

x(nT) = 5cos((2*pi*1000*n) /f_s)
x(nT) = 5cos((2000*pi*n)/8000)
x(nT) = 5cos((1/4)*pi*n) <-- This is where I get stuck.

I don't recall the Euler Method and I don't understand how they get -1 and 1, and it shows 2.5.

Am I doing this wrong and Eulor Identity is the only way to do this? Or is my procedure right the way I am doing it? Again if its correct, this is where I get stuck at.

I have homework problems that covers similar materials like this and if someone can help me understand this, that would great.

 

[Valkarie]

Thanks! The Euler Identity is a useful tool to use when trying to understand the Nyquist Sampling Theorem. You are correct in your procedure, but you are missing one step. To get -1 and 1, you need to use the trigonometric identity: cos(x) = (e^jx + e^-jx)/2. In this case, x = (1/4)*pi*n. Plugging this into the identity gives us:x(nT) = 5cos((1/4)*pi*n) = (e^j((1/4)*pi*n) + e^-j((1/4)*pi*n)) / 2At this point, you can simplify the equation by multiplying it by the constant 5:5x(nT) = (5e^j((1/4)*pi*n) + 5e^-j((1/4)*pi*n)) / 2Now, since e^jx and e^-jx are always equal to 1 and -1, respectively, we can rewrite the equation as:5x(nT) = (5(-1) + 5(1)) / 2 = 2.5(-1) + 2.5(1)And this gives us the same result as the Euler Identity. Hope this helps!