PainterGuy
- 938
- 72
Hi,
I was trying to find the magnitude of DC signal in a shifted unit pulse signal. The unshifted pulse lasts from -π to π and then it is shifted by π duration.
In Method #1 I have used FT formula and ended up with magnitude of 6.2832 for DC signal, i.e. ω=0.
In Method #2 I have used Laplace transform to derive the FT by setting σ=0 and ended up with magnitude of 6.5938 for the DC signal, i.e. ω=0.
What is contributing toward the error of 6.5938-6.2832=0.3106?
Could you please help me with it? Thank you!
Method #1:

Finding magnitude of DC signal:
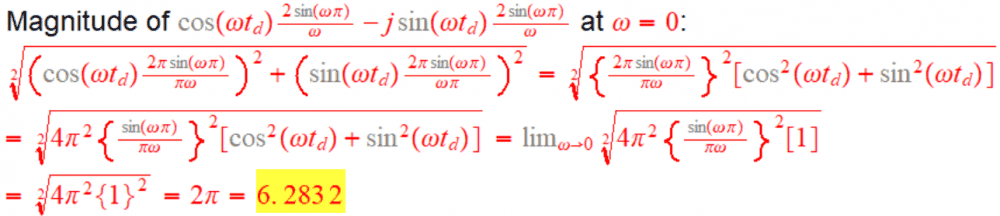 Method #2:
Method #2:
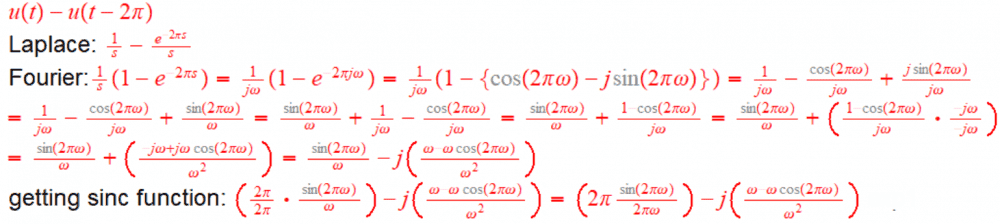
Finding magnitude of DC signal:
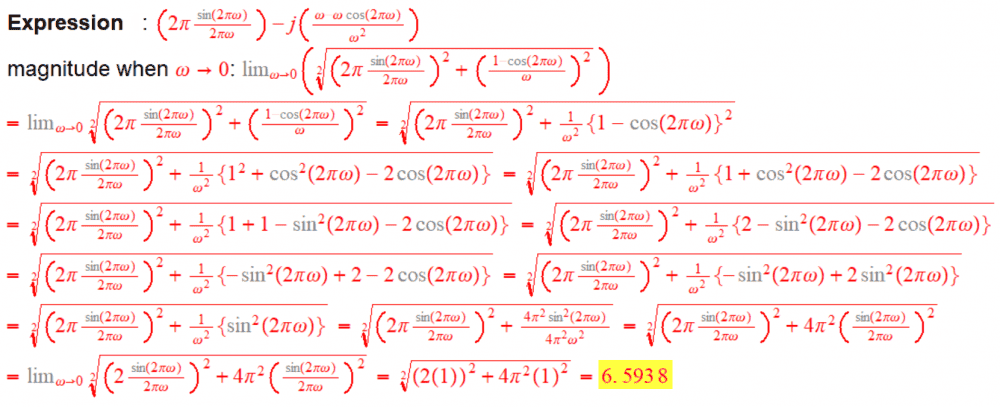
I was trying to find the magnitude of DC signal in a shifted unit pulse signal. The unshifted pulse lasts from -π to π and then it is shifted by π duration.
In Method #1 I have used FT formula and ended up with magnitude of 6.2832 for DC signal, i.e. ω=0.
In Method #2 I have used Laplace transform to derive the FT by setting σ=0 and ended up with magnitude of 6.5938 for the DC signal, i.e. ω=0.
What is contributing toward the error of 6.5938-6.2832=0.3106?
Could you please help me with it? Thank you!
Method #1:
Finding magnitude of DC signal:
Finding magnitude of DC signal:
Attachments
Last edited: