Obtaining position in a dipole field

[IanBerkman]

Hi all,

Consider one has a magnetic dipole, the field given by:

\begin{equation}
\vec{B} = \frac{\mu_0}{4\pi}\left(\frac{3(\vec{m}\cdot\vec{r})\vec{r}}{r^5}-\frac{\vec{m}}{r^3}\right)
\end{equation}

where we can take $$\vec{m} = m\hat{y}$$.

Let us say we have the a magnet vector which is theoretically somewhere in the dipole field. Is it possible to obtain the location where that magnet vector occurs?

To simplify things a bit, I looked at the fieldlines of a dipole, sliced through the XY plane:

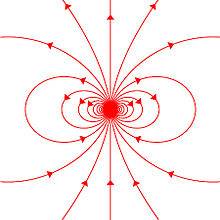
If we have a magnet vector of B = a[1,1,0], the vector would lie somewhere along the line y = 2x (just a really rough approximation to get my point across). The magnitude of the vector should correspond to two points on this line due to the symmetry. However, the dipole equation becomes

\begin{equation}
a[1,1,0]^\intercal = \frac{\mu_0m}{4\pi}\left(\frac{3y\vec{r}}{r^5}-\frac{\hat{y}}{r^3}\right)
\end{equation}

Which remains quite a tough equation to solve.

What am I missing in my line of reasoning?

 

[NFuller]

Let us say we have the a magnet vector which is theoretically somewhere in the dipole field. Is it possible to obtain the location where that magnet vector occurs?

I'm not sure if I understand your question. Are you asking that when given $\mathbf{B}$ at some location in space, if it is possible to determine the source location?

If that is your question then the answer is no. This is because for a simple magnetic dipole, the magnetic field will be uniform along a circular ring coaxial with the dipole. The problem is also under constrained considering that the field strength is a function of the dipole strength and the distance; you have neither.

 

[IanBerkman]

I'm not sure if I understand your question. Are you asking that when given $\mathbf{B}$ at some location in space, if it is possible to determine the source location?

If that is your question then the answer is no. This is because for a simple magnetic dipole, the magnetic field will be uniform along a circular ring coaxial with the dipole. The problem is also under constrained considering that the field strength is a function of the dipole strength and the distance; you have neither.

The magnetic field magnitude would be uniform along the circular ring coaxial with the dipole. However, the magnetic field vectors would be different along the ring.

Let us consider the same magnetic dipole again in the y-direction, and we know the field at a certain position is of the form B=[1,1,0]. Since this field has no z-component, the answer should lie in the XY-plane instead of on a circular ring.

The dipole strength is known since m is given.

 

[NFuller]

However, the magnetic field vectors would be different along the ring.

The magnetic field of a dipole $\mathbf{m}=m\hat{\mathbf{z}}$ in spherical coordinates is
$$\mathbf{B}=\frac{\mu_{0}m}{4\pi r^{3}}\left(2\text{cos}(\theta)\hat{\mathbf{r}}+\text{sin}(\theta)\hat{\mathbf{\theta}}\right)$$
Notice that there is no $\phi$ dependence here so the magnetic field has azimuthal symmetry. Thus $\mathbf{B}$ is constant along a ring coaxial with the z-axis.