- #1
altruan23
- 22
- 5
- Homework Statement
- I was analyzing the adder circuit and I dont understand from where does the - come in the Vout equation.
- Relevant Equations
- KCL
So i used KCL and both currents are flowing into the node, and then leaving together to go to the resistor R3.
So my eq can be seen in the picture. I was looking in a book and they had a minus infront of the parantheses.
Is the current flowing from R3 into the node??
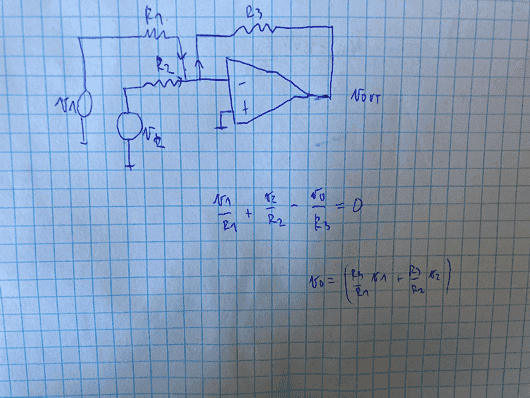
So my eq can be seen in the picture. I was looking in a book and they had a minus infront of the parantheses.
Is the current flowing from R3 into the node??