Optics (dealing with 2 sources of wavelength)

[jisbon]

Homework Statement

Two glass plates and a thread form an air wedge as shown below.
The glass plates are 10 cm long, and the thread is 0.05 mm in diameter.
When the wedge is illuminated by two wavelengths at 400 nm and 600 nm,
interference fringes appear. Determine the distance of the second dark fringe
from the contact point of the two glass plates

Relevant Equations

For phase change:
Destructive interference: $2nt=m\lambda$

To start off, I dealt with questions similar to this, but it only involves one wavelength. Now that there's 2 wavelengths, I'm kind of stumped as to what I should do.

Since the question stated a second dark fringe, I can assume that it will be a destructive interference. Since the rays are being reflected off the wedge, as shown below, there will be a phase change for the first ray and no phase change for the second ray, hence Destructive interference: $2nt=m\lambda$

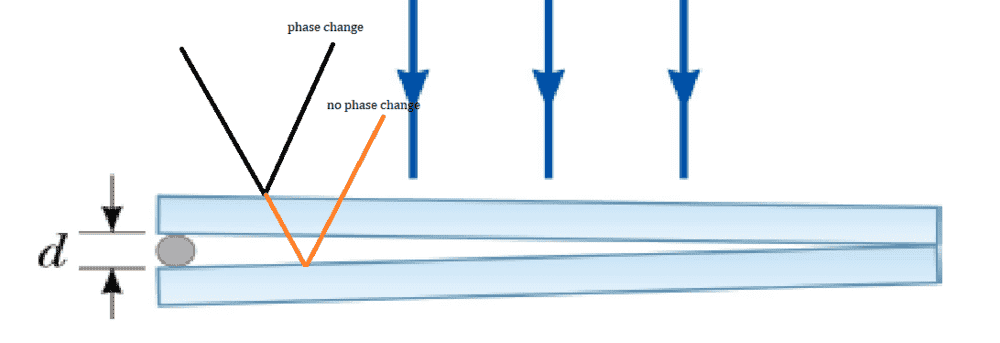
Let's say I deal with them 1 by 1,

For 400nm,

$2nt=m\lambda$
$2*1*t=m(400nm)$

and vice versa.

What should I do?

 

[kuruman]

The 400 nm light does not interfere with the 600 nm light. Since you understand the single wavelength problem, find the positions along the bottom plate of the first (no more than two) dark fringes for each wavelength and see which one is the second from the contact point. Note that you need to translate the fringe order $m$ into a length.

Also, your picture is misleading. The reflection of the black ray should be drawn off the back surface of the top plate not the front. The "thin film" is the air gap between the plates.