Optics mirrors problem with rearview of car

In summary, the conversation discusses the visibility of a car behind while driving. It mentions the distance of the eye from the rearview mirror, the size of the car behind, and the length of the mirror. The solution involves using reflection laws and similar triangles to determine if the entire car can be seen. However, there is some confusion about the measurements and the accuracy of the diagram provided.
  • #1
alingy1
325
0

Homework Statement


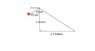
I'm riding my car. My eye is 40cm from the rearview mirror. I want to know if I can see the car behind me. The car behind me is 2.5m large. Can I entirely see the car behind me in his whole wideness? The mirror is 23 cm long. The car is 4 meters behind us.


Homework Equations


Reflection laws.
Similar triangles.


The Attempt at a Solution


So, I drew this triangle (look attachment). And found that the eye, from where he his, can see the whole car. But, the question is not too clear. Do you think my steps are good?
 

Attachments

  • Photo pour Yu2.jpg
    Photo pour Yu2.jpg
    7 KB · Views: 443
Physics news on Phys.org
  • #2
Where is the 4 meters measured from, the eye or the 23 cm mirror ? I think you have the correct answer though, at least app[roximately.
 
  • #3
Your diagram is confusing and not accurate. The triangles are not similar.
40/23 is not equal to 4/2.5
 

1. How does a rearview mirror work?

A rearview mirror uses a flat or convex mirror to reflect light from objects behind the car into the driver's field of view. The mirror is angled in such a way that it allows the driver to see a wider view of the road behind them without having to turn their head.

2. Why do some rearview mirrors have a day/night mode?

Day/night mode on a rearview mirror is designed to reduce glare from headlights of cars behind you during nighttime driving. It works by tilting the mirror slightly to reduce the amount of light that reflects into your eyes.

3. How do convex mirrors improve visibility?

Convex mirrors are curved outward and have a wider field of view compared to flat mirrors. They allow drivers to see a larger area behind their car, making it easier to spot objects or other vehicles that may be in a blind spot.

4. Why do some cars have two rearview mirrors?

Two rearview mirrors are often found in larger vehicles, such as trucks and buses, to provide a better view of the road behind them. The second mirror, usually mounted on the passenger side, allows the driver to see more of their surroundings and potential blind spots.

5. Can you adjust the position of a rearview mirror?

Yes, you can adjust the position of a rearview mirror to fit your height and seating position. This ensures that you have a clear view of the road behind you while driving. Most rearview mirrors can be adjusted by moving the mirror itself or by using a lever or button on the mirror's base.

Similar threads

Two concave mirrors on a table
    • Introductory Physics Homework Help
Replies
7
Views
904
Method of mirroring - metal plates
    • Introductory Physics Homework Help
Replies
11
Views
690
Combined lens & mirror system
    • Introductory Physics Homework Help
Replies
1
Views
4K
Optics - spherical and plane mirror
    • Introductory Physics Homework Help
Replies
3
Views
3K
An analytic expression to describe spherical aberration
    • Introductory Physics Homework Help
Replies
2
Views
997
Mirror: refractive index and thickness
    • Introductory Physics Homework Help
Replies
1
Views
2K
Can You Focus on Two Distances at Once?
    • Introductory Physics Homework Help
Replies
1
Views
1K
Virtual and real image with concave mirror at 45 degrees
    • Optics
Replies
4
Views
1K
Mirror Falling: How Long Can Person See Their Feet?
    • Introductory Physics Homework Help
Replies
11
Views
904
How do similar triangles help determine the visible area in a plane mirror?
    • Introductory Physics Homework Help
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top