Glen Maverick
- 14
- 0
Expected value: urgent help needed
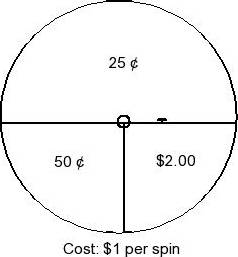
"Spin-and-Win" is under new management. The new management has created the spinner to the right and now charges $1 per spin. (The person spinning wins the amount pointed to by the spinner.)
a) What is the expected value for this game?
b) What does your answer in part 'a' mean for the owner/manager, if there are 1000
customers who play the game in a week?
I tried and produced two different solutions, and I don't know which one is right!
Trial 1:
a) expected value for the player
= 0.25*1/2 + 0.50*1/4 + 1*1/4 - 1
= (-) $0.50
b) for the owner, the expected value is (+) $0.50
so , assuming each customer plays once,
he will gain 1000*0.50
= $500/wk
Trial 2:
Customers expected winnings = (1/2)*$0.25 + (1/4)*$0.5 + (1/4)*$2 - $1 = - $0.25
This means the owner makes a profit of 25c per customer on average, so $250 in an average week of 1000 customers.
---------------------------------------------
Could you please check for me? I am so confused!
Homework Statement
"Spin-and-Win" is under new management. The new management has created the spinner to the right and now charges $1 per spin. (The person spinning wins the amount pointed to by the spinner.)
a) What is the expected value for this game?
b) What does your answer in part 'a' mean for the owner/manager, if there are 1000
customers who play the game in a week?
Homework Equations
The Attempt at a Solution
I tried and produced two different solutions, and I don't know which one is right!
Trial 1:
a) expected value for the player
= 0.25*1/2 + 0.50*1/4 + 1*1/4 - 1
= (-) $0.50
b) for the owner, the expected value is (+) $0.50
so , assuming each customer plays once,
he will gain 1000*0.50
= $500/wk
Trial 2:
Customers expected winnings = (1/2)*$0.25 + (1/4)*$0.5 + (1/4)*$2 - $1 = - $0.25
This means the owner makes a profit of 25c per customer on average, so $250 in an average week of 1000 customers.
---------------------------------------------
Could you please check for me? I am so confused!