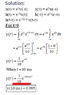Output of transfer function given impulse response and input the

[jaus tail]

Homework Statement

Homework Equations

Find laplace of x(t) and h(t)
Multiply the laplaced values to get Y(s)
Find inverse laplace to get y(t)

The Attempt at a Solution

In book the circled term isn't there. Why does that go away?
Book gets y(t) as

In laplace why does the e^5t term go away?

 

[rude man]

You will fin that the answer derives from the convolution integral. That method is valid for all time -∞ < t < ∞. The Laplace transform you're familiar with is most likely the one-sided Laplace transform which assumes x(t) = 0 for t < 0, so not applicable here.

There are two other alternatives: the Fourier transform and the two-sided Laplace transform. The latter is seldom encountered (see footnote) while the Fourier is appropriate and gives the same answer.

[Footnote: Then Brooklyn Poly's Professor John G. Truxal's venerable "Automatic Feedback Control System Synthesis" invokes it in preference to the Fourier].

 

[jaus tail]

Thanks. Convolution is better than the Fourier route.