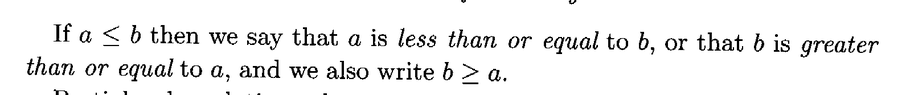MHB Partial Order .... Garling, pages 9-10, Volume I ,,,

  • Thread starter Thread starter Math Amateur
  • Start date Start date
  • Tags Tags
    Partial Volume
Click For Summary
Garling's definition of a partial order includes transitivity and a condition that implies anti-symmetry, but does not explicitly mention reflexivity. Some authors, like Cunningham, define a partial order to include reflexivity as a necessary property. However, it is suggested that reflexivity can be derived from Garling's conditions of transitivity and anti-symmetry. Upon closer examination, Garling's second condition implies that if two elements are equal, they are also related to themselves, thus satisfying reflexivity. This clarification resolves the confusion regarding the inclusion of reflexivity in Garling's definition.
Math Amateur
Gold Member
MHB
Messages
3,920
Reaction score
48
I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume I: Foundations and Elementary Real Analysis ... ...

I am focused on Chapter 1: The Axioms of Set Theory ... ...

I need some help to clarify an aspect of Garling's definition of a partial order ...Garling's definition of a partial order reads as follows:View attachment 9028
View attachment 9029Garling thus defines a partial order relation as possessing transitivity and anti-symmetry ... but a number of other authors define a partial order as having the property of reflexivity as well ...

... ... an example is Daniel W. Cunningham: Set Theory: A First Course ... who defines a partial order as follows:View attachment 9030Can someone explain why Garling does not include reflexivity in his definition of a partial order ...?

Is it perhaps that it is possible to derive reflexivity from transitivity and anti-symmetry ... but how do we do that ...?Help will be appreciated ...

Peter
 

Attachments

  • Garling - 1 - Defn of Partial Order - PART 1 .png
    Garling - 1 - Defn of Partial Order - PART 1 .png
    8.2 KB · Views: 149
  • Garling - 2 - Defn of Partial Order - PART 2 .png
    Garling - 2 - Defn of Partial Order - PART 2 .png
    3.4 KB · Views: 154
  • Cunningham - Defn of Partial Order ... .png
    Cunningham - Defn of Partial Order ... .png
    20.4 KB · Views: 145
Physics news on Phys.org
Note that the definitions of antisymmetry in Garling and Cunningham differ. Garling does not even call it antisymmetry.
 
Evgeny.Makarov said:
Note that the definitions of antisymmetry in Garling and Cunningham differ. Garling does not even call it antisymmetry.
Oh! Indeed, Evgeny ... think I see what you mean ...

After transitivity, Garling's second condition for a partial order is as follows:

(ii) $$a \leq b$$ and $$b \leq a \ \ $$ if and only if $$ \ \ a = b$$ ... so if $$a = b$$ we have $$a \leq a$$ ... that is, we have reflexivity ... I should have read Garling's condition more carefully ... Thanks for the help, Evgeny ...

Peter
 

Thread 'About the definition of topological manifold using closed sets'

We all know the definition of n-dimensional topological manifold uses open sets and homeomorphisms onto the image as open set in ##\mathbb R^n##. It should be possible to reformulate the definition of n-dimensional topological manifold using closed sets on the manifold's topology and on ##\mathbb R^n## ? I'm positive for this. Perhaps the definition of smooth manifold would be problematic, though.
View full post »

Similar threads

MHB The Annihilator of a Set ....Remarks by Garling After Proposition 11.3.5 ....
  • · Replies 2 ·
Replies
2
Views
2K
MHB Pseudometrics .... Garling, Proposition 11.1.13 .... ....
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Bounded in Norm .... Garling, Section 11.2: Normed Spaces ....
  • · Replies 2 ·
Replies
2
Views
2K
MHB Necessary and Sufficient Meaning of Isometries by D. J. H. Garling
  • · Replies 5 ·
Replies
5
Views
2K
MHB Bounded in Norm .... Garling, Section 11.2: Normed Spaces ....
  • · Replies 5 ·
Replies
5
Views
2K
MHB Prop 11.3.5-4: Peter's Help with Garling's The Annihilator of a Set
  • · Replies 3 ·
Replies
3
Views
1K
MHB How Do We Know the Annihilator Operation Is Associative?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Orthogonal Projections .... Garling, Proposition 11.4.3 .... ....
  • · Replies 2 ·
Replies
2
Views
2K
MHB Normed and Inner Product Spaces .... Garling, Corollary 11.3.2 ....
  • · Replies 2 ·
Replies
2
Views
1K
MHB Gram-Schmidt Orthonormalization .... Garling, Corollary 11.4.2 ....
  • · Replies 2 ·
Replies
2
Views
1K