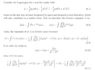- #1
Woolyabyss
- 143
- 1
I'm having trouble understanding a specific line in my lecturers notes about the path integral approach to deriving the Klein Gordon propagator. I've attached the notes as an image to this post. In particular my main issue comes with (6.9). I can see that at some point he integrates over x to get a Dirac delta, which is how he gets the minus p's. I'm just not certain how he gets the desired dirac dellta function to make this expression? When I do the calculation I end up with 𝛿 (2p). Any help would be appreciated.