DannoXYZ
- 69
- 16
Pedal-force for bicycle @ 43.2mph ?
I heard that bike-racers can put put 1500 watts in sprints. Using this site: http://www.noping.net/english and entering the following:
- Racing bike - hands on the drops
- weight = 170 lbs
- power = 1500 watts
Then hit CALCULATE button and I get a speed of 43.2mph. I came up with this diagram to figure out all the forces and torques in order to come up with pedal-force:
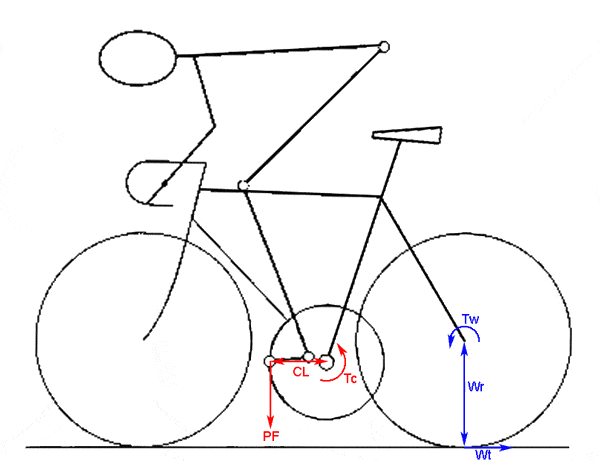
0.336m = Wr = Wheel Radius
0.170m = CL = Crank length
Given 52x13t gear ratio of 4:1, Tc = 4*Tw; torque at crank is 4x higher than torque at wheels.
Then using this site: http://www.analyticcycling.com/GearCadenceSpeed_Page.html, I enter:
speed = 43.2mph
chainring = 53t
cog = 13t
wheel-diameter = 0.672m
Click on RUN MODEL and I get 135 rpms at the crank.
What stops me next is how to figure out what PF - pedal force is in order to generate 1500w and go 43.2mph @ 135rpms. ?
Thanks.
I heard that bike-racers can put put 1500 watts in sprints. Using this site: http://www.noping.net/english and entering the following:
- Racing bike - hands on the drops
- weight = 170 lbs
- power = 1500 watts
Then hit CALCULATE button and I get a speed of 43.2mph. I came up with this diagram to figure out all the forces and torques in order to come up with pedal-force:
0.336m = Wr = Wheel Radius
0.170m = CL = Crank length
Given 52x13t gear ratio of 4:1, Tc = 4*Tw; torque at crank is 4x higher than torque at wheels.
Then using this site: http://www.analyticcycling.com/GearCadenceSpeed_Page.html, I enter:
speed = 43.2mph
chainring = 53t
cog = 13t
wheel-diameter = 0.672m
Click on RUN MODEL and I get 135 rpms at the crank.
What stops me next is how to figure out what PF - pedal force is in order to generate 1500w and go 43.2mph @ 135rpms. ?
Thanks.
Last edited by a moderator: