Bicycles and Mechanical Advantage

[UMath1]

I am trying to understand how mechanical advantage works in a bicycle but I am still a little confused.

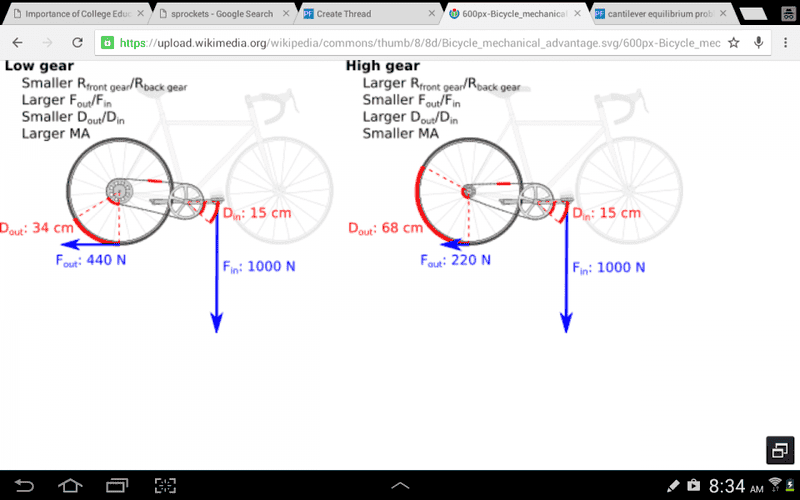
I understand that the force applied to the pedal goes first to the crank sprocket which then applies a force to the chain at its radius which is the then applied to the gear at the wheel. While the force applied is same in either case, the torque is not. Because the big gear has a larger radius, it would receive a greater torque. What I don't understand, however, is why is that there is a greater output force with the larger gear? And also I don't quite understand why a greater output force is beneficial.

 

[Orodruin]

What I don't understand, however, is why is that there is a greater output force with the larger gear?

When you apply a force to the pedals, this results in a tension in the chain. Depending on the moment arm at the back gear, this tension will result in different torques. If the moment arm is larger, you will obtain a larger torque and therefore a larger force transferred to the rim of the back wheel (whose moment arm is fixed to the wheel radius).

And also I don't quite understand why a greater output force is beneficial.

Did you every try to ride a bike uphill?

 

[FactChecker]

Because the big gear has a larger radius, it would receive a greater torque. What I don't understand, however, is why is that there is a greater output force with the larger gear?

Because the greater torque will turn the wheel with a greater force. You may be confusing force with work. All else being equal, the work is identical for the large and small gear. Work is Force times Distance (W=F*D). For different sized gears, there is a trade off between force and distance that keeps the work constant.

And also I don't quite understand why a greater output force is beneficial.

It isn't necessarily better. In simple machines, there is a trade off between force and distance. Work is force times distance, so the amount of work remains the same in that trade off. You want the combination of force and distance that gives the greatest efficiency. That is an entirely different consideration. If you are riding a bike up hill, you want a gear that gives you more force to climb the hill even if you are going slower (more force, but less distance for each pedal stroke). But if you are riding down hill, you want a gear that gives you more speed even if it gives you less force (more distance for each pedal stroke, but less force). You want the combination of force and distance that matches your situation best.

 

[UMath1]

I don't understand why a larger torque will turn the wheel with greater force though. The gear is attached to the wheel. So when a bigger gear is used, you have more torque on the wheel resulting in great angular acceleration. But how does that mean more force?

For my second question, what I mean is I don't quite understand how a bicycle moves forward. From what I understand the wheel applies a force on the ground (friction) backwards, and the ground applies a force back on the wheel (friction). Is this right? Can someone explain exactly how this works? But building on that, how would more force be beneficial when riding uphill? Only friction contributes to torque, not gravity.

 

[FactChecker]

I don't understand why a larger torque will turn the wheel with greater force though. The gear is attached to the wheel. So when a bigger gear is used, you have more torque on the wheel resulting in great angular acceleration. But how does that mean more force?

You are skipping a step here. More torque does not automatically lead to greater angular acceleration. What if the wheel is held fixed? The first step is that more torque means more force (torque IS force). If that force is not opposed, then F=MA means that greater force leads to greater acceleration.

For my second question, what I mean is I don't quite understand how a bicycle moves forward. From what I understand the wheel applies a force on the ground (friction) backwards, and the ground applies a force back on the wheel (friction). Is this right?

Yes.

Can someone explain exactly how this works? But building on that, how would more force be beneficial when riding uphill? Only friction contributes to torque, not gravity.

You are skipping an important step in your thinking. Friction of tires is complicated, but we can simplify and assume that there is enough friction to keep the wheel from slipping. Then the friction is essentially static friction. Static friction supplies exactly enough force to oppose the force trying to make the tire slip. So static friction force and the force to move (slip) are equal and opposite. That is how the gear force turns into a force to go up hill: gear force => tire force => force trying to make tire slip => - static friction force => force to go up hill.

 

[UMath1]

You are skipping a step here. More torque does not automatically lead to greater angular acceleration. What if the wheel is held fixed? The first step is that more torque means more force (torque IS force). If that force is not opposed, then F=MA means that greater force leads to greater acceleration.

How does more torque mean more force? Torque is R × F. In the diagram above, in the case of both the small gear and the big gear, the input force is 1000 N. So the only reason torque is more in the big gear as far as I understand is that there is a bigger moment arm. Then I understand that if the torque is unopposed, then T= IA means that the greater torque leads to greater angular acceleration.

Static friction supplies exactly enough force to oppose the force trying to make the tire slip. So static friction force and the force to move (slip) are equal and opposite.

What is the force trying to make it slip? I know its kind of messy, but is this how the FBD would look?

Also, if this is correct, I don't understand why the slipping force is freater uphill. And in order for friction to produce cw torque it must be in this direction. But then wouldn't that mean that the force of the bicycle wheel must be in the opposite direction? How can that be?

 

[UMath1]

If the moment arm is larger, you will obtain a larger torque and therefore a larger force transferred to the rim of the back wheel (whose moment arm is fixed to the wheel radius).

I understand the fact that there will be a larger torque, but how does that equate to a larger force? The input force is the same in both gears. The only reason torque is greater in the larger gear is because it has a larger moment arm. Perhaps what I need to understand is how exactly does the gear transfer the force to wheel?

 

[FactChecker]

I should have said the static force exactly opposes the force trying to rotate the tire. (Without static friction, the force rotating the tire would cause it to slip.)

 

[UMath1]

If the force from the wheel is what makes it slip, why do you need more force from the wheel when going uphill?

And how exactly, does more torque mean more output force?

 

[crador]

T=IA doesn't apply here, you have no idea about the wheel's moment of inertia and it isn't free to rotate (it has to move the bicycle forward to rotate.

Some force in the form of tension in the chain will be supplied from the front gear to the back gear. If the back gear is small it will transmit a small force to the wheel of much larger radius, but be able to rotate the wheel much more over the same length of chain rotating it. If the back gear is large, larger force and less rotation per chain length.

In terms of basic physics you are supplying the same power, but choosing if you want it in terms of a big force times a small velocity (starting to pedal from standstill, you take off) or a small force at high velocity (maintaining speed onceunder way).

You can't always choose the bigger force to speed on happily, as your legs don't have the power to supply large forces at high velocities (you can't keep up with the spinning of the wheel if you are in low gear).

Clear?

 

[crador]

If the force from the wheel is what makes it slip, why do you need more force from the wheel when going uphill?

And how exactly, does more torque mean more output force?

The wheel doesn't slip normally. You need more force to combat gravity.

More torque on the wheel of fixed radius means more output force, by definition. You are trying to spin the wheel harder.

 

[UMath1]

More torque on the wheel of fixed radius means more output force, by definition. You are trying to spin the wheel harder.

I think what I don't understand is how the gear transmits the force to the wheel. See in both cases, that of the small and big gear, the force transmitted to the gear is 1000 N. The big gear has a bigger moment arm so it receives more torque. Since the gear is attached to the wheel, both, the gear and the wheel, undergo the same angular acceleration. So how does that mean there's a bigger force?

The wheel doesn't slip normally. You need more force to combat gravity

I don't think I understand the exact mechanics of this. Is this what is going on?

If this is what's going on, then static friction supplies the angular acceleration needed for going up the hill. Where does gravity and the force applied by the bicycle come into play?

 

[Orodruin]

You really need to work on your free body diagrams. In this case, you have not shown which body you are making a free body diagram of. Is it the wheel or the ground? The force from the ground on the wheel is in the forward direction. And slipping really is not a force.

 

[UMath1]

You really need to work on your free body diagrams. In this case, you have not shown which body you are making a free body diagram of. Is it the wheel or the ground? The force from the ground on the wheel is in the forward direction. And slipping really is not a force.

The diagram is on the wheel. Wouldn't the force from friction be in the backward direction in order to supply clockwise torque though? And what would be the force that creates the slipping then? Or is slipping a lack of force?

 

[Orodruin]

The diagram is on the wheel. Wouldn't the force from friction be in the backward direction in order to supply clockwise torque though?

Then it is simply wrong. The torque in the clockwise direction is provided by the chain. The force from the ground on the wheel is what accelerates the entire bike in the end. It must be in the forward direction.

 

[UMath1]

Then it is simply wrong. The torque in the clockwise direction is provided by the chain. The force from the ground on the wheel is what accelerates the entire bike in the end. It must be in the forward direction.

Is this correct?

But if the force from the ground is forward, wouldn't it produce a ccw torque causing the wheel to roll in the opposite direction?

 

[Orodruin]

But if the force from the ground is forward, wouldn't it produce a ccw torque causing the wheel to roll in the opposite direction?

You are pedalling, this is what provides a cw torque. So now you can compute backwards. Assume you are going uphill at constant velocity, meaning there is force and torque balance. What is the torque you need to supply to the wheel through the chain? What is the corresponding force the chain must provide on the wheel?

 

[UMath1]

So it would be:

Fgx + Fwheel = Fground

Tground=Twheel

?

 

[Orodruin]

It is unclear what you mean by Twheel and Fwheel. Please define the symbols you are using, this is important not only to have others understand you, but also not to confuse yourself.

 

[UMath1]

Fwheel is the output force that the wheel applies on the ground. Twheel is the torque the chain applies on the gear.

 

[Orodruin]

Fwheel is the output force that the wheel applies on the ground. Twheel is the torque the chain applies on the gear.

Fwheel is then not part of the forces you should be considering, your free body diagram is for the wheel, not the ground! The forces on the wheel are: the force from the bike on the wheel, the force from the ground on the wheel, the gravitational force on the wheel, and the force from the chain on the wheel. In equilibrium, these should sum to zero. This also goes for your torques, I strongly recommend not having different directions for the torques and instead considering the torques negative if they act ccw and positive when acting cw.

 

[UMath1]

So then how is having a greater output force from the wheel beneficial in going uphill? How does it affect the other forces acting on the wheel?

And how does a greater torque in the gear equate to a greater output force?

 

[Orodruin]

Why don't you just compute the torque needed as suggested? You should find that it does not depend on the moment arm. However, since the torque is constant, you need to supply less force on the chain with a longer moment arm.

 

[crador]

I think what I don't understand is how the gear transmits the force to the wheel. See in both cases, that of the small and big gear, the force transmitted to the gear is 1000 N. The big gear has a bigger moment arm so it receives more torque. Since the gear is attached to the wheel, both, the gear and the wheel, undergo the same angular acceleration. So how does that mean there's a bigger force?
I don't think I understand the exact mechanics of this. Is this what is going on?
View attachment 85514
If this is what's going on, then static friction supplies the angular acceleration needed for going up the hill. Where does gravity and the force applied by the bicycle come into play?

This is basically all wrong. The force transmitted to any tooth of any gear is not 1000N. That is the force you are exerting on the pedal with some speed.

Force is not a fundamental thing that you are supplying. Fundamentally you are supplying power, and the levers you use determine how that power is partitioned between force and speed.

 

[crador]

Perhaps you should just review a unicycle before trying the bicycle. Say you have the pedals attached directly to the wheel. How would changing the length of the pedals change the force and torque on the wheel?

 

[UMath1]

Why don't you just compute the torque needed as suggested? You should find that it does not depend on the moment arm. However, since the torque is constant, you need to supply less force on the chain with a longer moment arm.

Is this correct? From what I understand the torque the chain applies on the wheel must equal the torque from static friction if the bicycle is traveling at constant velocity. Based on that I am able to determine the output force from the bicycle wheel.

But what about when the bicycle is trying to accelerate, is it friction or the chain that supplies the net force and net torque on the wheel? If friction is what supplies the net force, then wouldn't the bicycle roll backwards(friction would give a ccw torque)?

And what exactly happens when the bicycle slips down the hill? If you are in a small gear, then you have small output force which means you get less static friction. So then is it that because you get less static friction, gravity's x-component supplies a net force causing a downward acceleration?

 

[Chris42163]

The tire exerts a force onto the ground equal to 50N. It can also be said that the ground exerts a 50N force on the tire. If this is the only force acting on the bike in the x-direction, then the bike will accelerate in the x-direction. If not, then you must sum all of the forces acting in the X-direction. The bike will accelerate if there is any net force. Opposition forces include drag, and rolling resistance.

 

[UMath1]

The tire exerts a force onto the ground equal to 50N. It can also be said that the ground exerts a 50N force on the tire. If this is the only force acting on the bike in the x-direction, then the bike will accelerate in the x-direction. If not, then you must sum all of the forces acting in the X-direction. The bike will accelerate if there is any net force. Opposition forces include drag, and rolling resistance.

But isn't the force of the chain also acting on the wheel? And if the net force is provided by the ground, then how come the acceleration of the wheel is cw and not ccw?

 

[Chris42163]

You just gave the force of the chain acting on the wheel. How are you still confused about it? The chain simply transmits the linear force from one gear to the other. The radius of the gear about its fixed axis makes it a torque applied to the wheel, and the radius of the wheel changes it back into a linear force.

Also, I don't know what cw and ccw are. So, I can't answer that question, yet.

 

[Chris42163]

One of the things I think you're having problems with is your free body diagram. Free body diagrams are only meant to view a single body. I think you may be confusing the equal and opposite forces at work with some idea that they may be canceling each other out. They are not. In the end, the tire exerts a force on the ground at that force causes the acceleration of the bike as a system. There is no need to consider the ground, the chain, the foot on the pedal. Once you know that the force is being exerted out of the system, then you know that the system is accelerating.

There's a lot going on internally that gets that force to the tire, but looking at the system as a whole... as a single body, it is exerting a force, and as long as it is greater than the net forces acting against it, the system is undergoing acceleration.

So starting from the beginning with a bike and its rider. The rider exerts a 10 Newton force on a pedal that is 0.5m from its axis, then there is 5Nm of torque on the drive gear. If the drive gear's radius is 1/10 of a meter, the gear puts a 50N force on the chain. The 50N force is transferred via the chain to the rear gear. The rear gear is .5m. So, the torque transmitted to the wheel is 25Nm. The wheel is 1m. So the force between the tire at the road is 25N. This assumes adequate traction between the tire and road surface to transmit that force.

To determine the acceleration on the system, you will have to do some more work and gather some more facts. For instance, you'll need to know the mass of the rider and his bike. You will have to know the center of mass of the system. You'll have to break down the 25Nm force into it's X and Y components. Once you have them, you can calculate the acceleration in each direction, the shift of weight from front to rear, etc...

 

[UMath1]

I understand that, but in this I am considering the system to be the wheel, not the bike. So if the wheel is being considered, the force of the chain must be considered.

By cw and ccw, I mean clockwise and counterclockwise. So what I mean is, if the force of static friction from the ground is what provides the net force on the wheel, it must also therefore provide a net torque, right? And if that is true, wouldn't the acceleration of the wheel be counterclockwise instead if clockwise as it should be?

 

[A.T.]

if the force of static friction from the ground is what provides the net force on the wheel,

The net force on the wheel is the sum of all forces on the wheel.

it must also therefore provide a net torque, right?

No, same as above. The net torque on the wheel is the sum of all torques on the wheel.

 

[UMath1]

Yeah, but in order for the bicycle wheel to being moving, it must accelerate, meaning there must be both a net torque and net force.

 

[A.T.]

Yeah, but in order for the bicycle wheel to being moving, it must accelerate, meaning there must be both a net torque and net force.

To accelerate, not to move at constant speed.

 

[russ_watters]

Yeah, but in order for the bicycle wheel to being moving, it must accelerate, meaning there must be both a net torque and net force.

Sure, but until you have the simple case figured out, it is best not to move on to a more complicated one: stick to constant speed, where the torques sum to zero for now.