Percent Change Of current when the switch is closed

AI Thread Summary
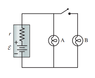
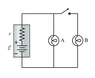
The discussion centers on calculating the percent change in current when a switch is closed in a circuit with a 1.50 V battery and internal resistance. Various calculations were attempted, yielding results of -3.86%, 4.02%, and others, all deemed incorrect. The issue arises from the practical observation that bulb A dims slightly when the switch is closed, despite theoretical expectations. The internal resistance of the battery and the resistance of the bulb are critical factors in understanding this behavior. A circuit diagram is requested to clarify the problem further.
ChrisWM
Messages
13
Reaction score
1
Homework Statement
By what percent does the current through A change when the switch is closed?

I found the value of the current to be .174 A when the switch is closed and value of the current when the switch is open to be .181 A.
Relevant Equations
final-initial/initial
(.174A-.181A)/.181A=-3.86% but it says it wrong, and I did (.181A-.174A)/.174A =4.02% but this was wrong too. I've tried 3.87%,3.86%,-3.87%,-3.67%,4.02%, and -4.02% but all were wrong. I'm really not sure what to do here.
 
Physics news on Phys.org
Is there a circuit diagram?
 
  • Like
Likes ChrisWM
1590556060734.png
Here you go!
 
Here is the actual problem; For an ideal battery (r = 0 Ω), closing the switch in (Figure 1)does not affect the brightness of bulb A. In practice, bulb A dims just a little when the switch closes. To see why, assume that the 1.50 V battery has an internal resistance r = 0.30 Ω and that the resistance of a glowing bulb is R = 8.00 Ω.
 

Attachments

  • 1590556104997.png
    1590556104997.png
    3.5 KB · Views: 171
cnh1995 said:
Is there a circuit diagram?
 

Attachments

  • 1590556762327.png
    1590556762327.png
    893 bytes · Views: 197

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Circuits and the percent change of current when the switch is closed
Replies
2
Views
2K
Current through circuit when switch is open
Replies
8
Views
4K
Voltmeter readings across a closed/open switch in circuits
Replies
10
Views
10K
Why a 20 Ohm lightbulb won't light up in a closed circuit?
Replies
7
Views
1K
Explain How the Lamp in Circuit A Lights When Switch S is closed
Replies
13
Views
2K
RL circuit after switch has been opened
Replies
6
Views
2K
Calculate resistance if the switch is closed 2 battery with different voltage
Replies
6
Views
3K
Current in a capacitor question
Replies
6
Views
2K
Current in circular wire surrounding infinite solenoid in a circuit
Replies
7
Views
1K
Determining the Change in Bulb Brightness by Changing Circuit
Replies
6
Views
1K

Hot Threads

Recent Insights

Back
Top