furor celtica
- 69
- 0
Prove that, if (c - b).a = 0 and (c - a).b = 0, then (b - a).c = 0. Show that this can be used to prove the following geometric results:
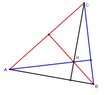
a. The lines through the vertices of a triangle ABC perpendicular to the opposite sides meet in a point.
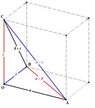
b. If the tetrahedron OABC has two pairs of perpendicular opposite edges, the third pair of edges is perpendicular.
Prove that also, in both cases, (OA)^2 + (BC)^2 = (OB)^2 + (CA)^2 = (OC)^2 + (AB)^2So for the very first task I proceeded by attributing coordinates to each vector: a = (x(1), y(1), z(1)), b = (x(2), y(2), z(2), c = (x(3), y(3), z(3)), where the numbers are actually at the bottom left of the coordinates, but I don't know how to use that notation here.
Anyway I could post all my work but it would take a long time; I didn't have much of a problem at all with the first task and proved that (b - a).c = 0. It took a while though, as you can imagine; is there another way to solve problems like this, or does one always have to use attributed coordinates and deal with those?
With a. and b. I'm stuck, however.
a. I usually would try to solve a question like this by taking into account the end result and what exactly I'm supposed to end up with (and often work backwards to return to the given results), but here I'm not sure at all what you end up with algebraically when three vectors meet. What am I looking for? Also I'm confused on how to find the vectors that are perpendicular to the opposite sides, how to formulate them with regard to the coordinates of A, B and C.
b. Here I immediately became confused as to what is meant by 'opposite edges'. But besides that it seems to be a fairly straightforward variation of the very first task, am I correct?
The last task seems simple as well, as I would just take the attributed coordinates and reformulate the magnitudes of the given vectors to be equivalent, perhaps with some help from the result in the first task. I haven't tackled this one yet.
a. The lines through the vertices of a triangle ABC perpendicular to the opposite sides meet in a point.
b. If the tetrahedron OABC has two pairs of perpendicular opposite edges, the third pair of edges is perpendicular.
Prove that also, in both cases, (OA)^2 + (BC)^2 = (OB)^2 + (CA)^2 = (OC)^2 + (AB)^2So for the very first task I proceeded by attributing coordinates to each vector: a = (x(1), y(1), z(1)), b = (x(2), y(2), z(2), c = (x(3), y(3), z(3)), where the numbers are actually at the bottom left of the coordinates, but I don't know how to use that notation here.
Anyway I could post all my work but it would take a long time; I didn't have much of a problem at all with the first task and proved that (b - a).c = 0. It took a while though, as you can imagine; is there another way to solve problems like this, or does one always have to use attributed coordinates and deal with those?
With a. and b. I'm stuck, however.
a. I usually would try to solve a question like this by taking into account the end result and what exactly I'm supposed to end up with (and often work backwards to return to the given results), but here I'm not sure at all what you end up with algebraically when three vectors meet. What am I looking for? Also I'm confused on how to find the vectors that are perpendicular to the opposite sides, how to formulate them with regard to the coordinates of A, B and C.
b. Here I immediately became confused as to what is meant by 'opposite edges'. But besides that it seems to be a fairly straightforward variation of the very first task, am I correct?
The last task seems simple as well, as I would just take the attributed coordinates and reformulate the magnitudes of the given vectors to be equivalent, perhaps with some help from the result in the first task. I haven't tackled this one yet.