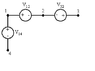Phasor to complex units

[DODGEVIPER13]

Homework Statement

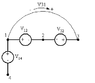
Several of the voltages associated with a certain circuit are given by V12=9∠30° V, V32=3∠132° V, V14=2∠10° V. Determine V21, V13, V34, and V24.

Homework Equations

The Attempt at a Solution

I am just using this problem as an example as I have no idea how to go from phasor to complex. So V13=V12+V32=9∠30°+3∠132°=? I don't really know here I can only imagine Magnitude*cos(θ)=Real and Magnitude*sin(θ)=imaginary I know this but how do I ultilize these beacuse everything I have done does not work?

 

[UltrafastPED]

Your first example is magnitude 9, phase angle 30 degrees. So the complex number is 9 x [cos(30) + j sin(30)]; this is what you have proposed. Make sure your calculator/computer is set to degrees, or else convert them to radians.

The alternative expression (in radians) may be more useful: use the Euler identity and write it as
9 exp(j*30/360*2pi).


Here is an example: http://people.clarkson.edu/~jsvoboda/eta/phasors/AddPhasors10.html

 

[DODGEVIPER13]

Ok thanks man

 

[DODGEVIPER13]

hey for V13 I get 5.865+j6.798 V

 

[DODGEVIPER13]

back in phasor I get 8.978∠49.21°

 

[DODGEVIPER13]

V21=V32+V13=3.936+j9.096

 

[DODGEVIPER13]

V34=V13+V14=7.834+j7.145 and V24=V32+V34=5.906+j9.443

 

[gneill]

V21=V32+V13=3.936+j9.096

As a reality check, note that you are given a value for V12. Shouldn't V21 = -V12?

 

[DODGEVIPER13]

oh heh so it should be V21=-9∠30° V

 

[DODGEVIPER13]

Also are the rest of my answers correct?

 

[gneill]

oh heh so it should be V21=-9∠30° V

Right. So if the method you employed previously doesn't result in that value, something may be amiss with your method. Better check into that.

Note that it's common practice to roll the "negative" into the angle in order to leave the magnitude positive. Add + or - 180° to the angle.

 

[gneill]

To keep things straight I'd suggest creating a little circuit fragment containing the "known" points and their given potential differences. Something like:

The voltage supply polarities reflect the subscript convention, namely V_ab would be the potential at a with respect to b, so that by convention a is where your meter's "+" lead would go and b would be where the "-" lead would go, if you were to make the measurement V_ab. The actual values assigned to the supplies may be positive or negative depending upon what you're given.

Then, to find any potential difference between points, perform the "KVL walk" between them and sum the potential changes.

 

[DODGEVIPER13]

so for V13=V12+V32

 

[gneill]

so for V13=V12+V32

By convention V13 would be the potential at 1 with respect to 3. So start at 3 and "walk" to 1. Pay attention to the polarities of the sources along the way.

 

[DODGEVIPER13]

Ahhh woops V13=V12-V32

 

[DODGEVIPER13]

V34=sqrt((V14)^2+(V32)^2+(V12)^2) right?

 

[DODGEVIPER13]

or should it be V34=sqrt(-(V14)^2+(V32)^2+(V12)^2)

 

[DODGEVIPER13]

hmmmmmmm V31=V32-V12 so that V34=V31-V41

 

[gneill]

V34=sqrt((V14)^2+(V32)^2+(V12)^2) right?

What are you trying to accomplish? The individual voltages are in complex form and you can sum them by summing their real and imaginary components separately.

If you want the magnitude of the result, then do the square root of the sum of the squares of its components.

 

[DODGEVIPER13]

so I solved V13=9.801+j2.271

 

[DODGEVIPER13]

I was trying to use Pythagorean Theorem which I know is incorrect sorry

 

[DODGEVIPER13]

did you read my new post after that is that close to how to solve for V34

 

[DODGEVIPER13]

more specifically post #18

 

[gneill]

did you read my new post after that is that close to how to solve for V34

more specifically post #18

I think you're still tripping over the directions of the potential changes. If you calculate a new potential difference, like V31, add a new branch to the diagram with the appropriate label and source direction. You can just use arrows to indicate polarity if the diagram starts getting too cluttered.

So for V34 you would start at V4 and walk through +V14 and +V31, right?

 

[DODGEVIPER13]

ok well V31=V32-V12=-9.801-j2.271

 

[DODGEVIPER13]

then V34=V14+V31

 

[DODGEVIPER13]

-7.831-j1.923=V34 hopefully?

 

[gneill]

-7.831-j1.923=V34 hopefully?

That looks okay.

 

[DODGEVIPER13]

V24=-V12+v14 = -5.824-j4.152