- #1
crick
- 43
- 4
In the experiment of the determination of ##h## using the photoelectric effect produced by light emitted by led's there is the systematic problem of the "dark current" or "back current", i.e. the current caused by photoelectric effect on the anode of the system which is used in the expreriment.
This current is opposite to the "normal" photocurrent and its effect is to make the I-V curves not going but keep decreasing (slightly).
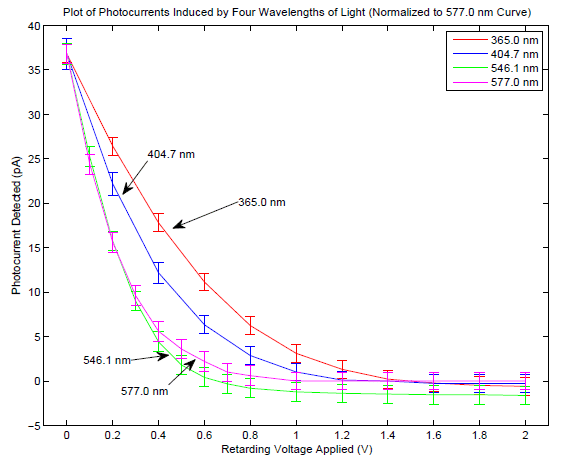
Suppose that one wants to determine $h$ using two different led's of frequencies ##\nu_1## and ##\nu_2## using the following method (I know about other methods but I would like to know about this one).
Let's call ##V_{0_1}## and ##V_{0_2}## the values of ##V## where the (total) photocurrent is ##0## (for led ##1## and led ##2##). And suppose that the relation used is $$h=\frac{e(V_{0_1}-V_{0_2})}{(\nu_2-\nu_1)} \tag{1}$$
(work function is not involved at all)
My question is: under what theoretical assymptions and explanations is ##(1)## suitable to calculate ##h## (i.e. when to determine ##V_0##, even if current does not go asymptitically to zero but becomes negative, is still a good method to determine $h$ using ##(1)##)?
My guess is that this is a "good" method only if ##V_0##Vis such that it "brakes" all the electrons always in the same way, i.e. it makes them reach the same kinetic energy, for any frequency ##\nu## that is being used.
But how is this confermed/denied theoretically?
This current is opposite to the "normal" photocurrent and its effect is to make the I-V curves not going but keep decreasing (slightly).
Suppose that one wants to determine $h$ using two different led's of frequencies ##\nu_1## and ##\nu_2## using the following method (I know about other methods but I would like to know about this one).
Let's call ##V_{0_1}## and ##V_{0_2}## the values of ##V## where the (total) photocurrent is ##0## (for led ##1## and led ##2##). And suppose that the relation used is $$h=\frac{e(V_{0_1}-V_{0_2})}{(\nu_2-\nu_1)} \tag{1}$$
(work function is not involved at all)
My question is: under what theoretical assymptions and explanations is ##(1)## suitable to calculate ##h## (i.e. when to determine ##V_0##, even if current does not go asymptitically to zero but becomes negative, is still a good method to determine $h$ using ##(1)##)?
My guess is that this is a "good" method only if ##V_0##Vis such that it "brakes" all the electrons always in the same way, i.e. it makes them reach the same kinetic energy, for any frequency ##\nu## that is being used.
But how is this confermed/denied theoretically?