Photon Wavelength of He+ Emission Spectrum

[CFXMSC]

Homework Statement

An electron of wavelength 1.74 \times 10^{-10} m strikes an atom of ionized helium (He+). What is the wavelength (m) of the light corresponding to the line in the emission spectrum with the smallest energy transition?

Homework Equations

Kinetic Energy

E_k=\frac{1}{2} \times m_e \times v_e^2

Photon Energy

E_p=\frac{h \times c}{\lambda_p}

Transition Energy

E_b=-k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)

De Broglie wavelenght

v_e=\frac{h}{m_e \times \lambda_e}

Constants:

h=6.6260755 \times 10^{-34} J s
c=299792458 \ m/s
m_e=9.1093897 \times 10^{-31} \ kg
k=2.1789601284 \times 10^{-18}
Z_{He^+}=2

Problem constant:

\lambda_e=1.74 \times 10^{-10}
n_i=?
n_f=?

The Attempt at a Solution

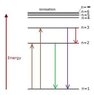
When the question say "smallest energy transition" what value of n_i=? and n_f=? should i use?

jumping this part and using energy balance i got that the kinetic energy of the electron must be equal to the transition energy plus photon energy:

\frac{1}{2} \times m_e \times v_e^2=-k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)+\frac{h \times c}{\lambda_p}

\frac{1}{2} \times m_e \times \left(\frac{h}{m_e \times \lambda_e}\right)^2=-k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)+\frac{h \times c}{\lambda_p}

Solving for \lambda_p

\lambda_p=\left[\frac{1}{2} \times m_e \times \left(\frac{h}{m_e \times \lambda_e}\right)^2 + k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\right]^{-1}\times h \times c

I've tryed for n_i and n_f 2 and 1, 3 and 2, 4 and 3 but without the right answer. What's wrong?

 

[TSny]

Your energy conservation equation is not correct. Maybe you're trying to do too much in one equation. The incoming electron must first bump the electron in the helium ion into an excited state. What does conservation of energy look like for this process?

 

[CFXMSC]

Why is it wrong?
The incoming electron energy is supposed to be equal to the emission spectrum energy and transition state energy.
I didn't get your point.

 

[TSny]

Why is it wrong?
The incoming electron energy is supposed to be equal to the emission spectrum energy and transition state energy.
I didn't get your point.

I'm not sure which transition state energy you're referring to here. There's an initial transition of the helium atom into an excited state by the incoming electron. Then there's the transition of the excited ion to a lower state associated with the emission of the photon. There's also the overall transition from the initial state of the ion before being hit by the electron to the final state of the ion after the photon is emitted.

Is it correct to assume that 100% of the incoming electron energy is absorbed by the helium atom? Since the energy states of the ion are quantized, only certain definite amounts of energy can be absorbed by the ion. Does the energy of the incoming electron match one of these possible energies that can be absorbed by the ion?

 

[CFXMSC]

Since the problem does not give the efficiency I've been considering 100%. I think i got you point now.

\frac{1}{2}\times m_e \times v_e^2 = k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right) [1]

Solve for n_f

Then

k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)=\frac{h \times c}{\lambda_p} [2]

Solve for \lambda_p with n_f from equation 1 equal to n_i in equation 2

 

[TSny]

The incoming electron might scatter off the ion transferring just a part of its kinetic energy to the ion. Thus, there could be several possibilities for how "high" the ion gets excited. The ion might only get excited to the first excited state, or maybe the second excited state, etc.

You need to decide which excited state the ion can be excited to in order for it to subsequently emit a photon of smallest possible energy.

 

[CFXMSC]

the question should give me this information, should not?

 

[TSny]

the question should give me this information, should not?

The question gives you sufficient information to figure it out. You've shown that you know how to calculate the energy of the incoming electron. What are the possible excited states of the ion that can result from being hit by the electron?

 

[CFXMSC]

That is the point. i don't know how to do it

 

[TSny]

That is the point. i don't know how to do it

From a previous post you had an equation [1]:

\frac{1}{2}\times m_e \times v_e^2 = k \times z^2 \times \left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right) [1]

This equation assumes that all of the kinetic energy of the electron is transferred to the ion. Go ahead and assume this is true for now. What do n_i and n_f mean? Do you know the value of either one of these at the beginning? Can you then use the equation to solve for the other one?

 

[CFXMSC]

ni represents the ground state = 1

Solving for nf

nf=3.38654

What do i do with the decimal part?

 

[TSny]

ni represents the ground state = 1

Solving for nf

nf=3.38654

Good.

What do i do with the decimal part?

Give it some thought. Remember that your equation assumes all the energy of the incoming electron is transferred to the ion. Since you didn't get an integer value for n_f, what does that tell you?

 

[CFXMSC]

It means that the energy provided by the electron is sufficient to raise the energy level up to level 3 and little bit more.

Right?

 

[TSny]

OK, but the ion cannot accept a "little bit more". So, what are the possible excited states that the ion could get excited to by the incoming electron?

 

[CFXMSC]

level 3?

 

[TSny]

Level 3 is one possibility. But that's not the only possible excited state that the ion could get excited to.

 

[CFXMSC]

i can't imagine another level.

 

[TSny]

Does the incoming electron have enough energy to excite the ion from the ground state to the n = 2 state? From the ground state to the n = 4 state?

 

[CFXMSC]

The electron has energy to excite from ground state to n=2 and 3. Does the smallest transition occurs from 3 to 2?

 

[TSny]

Yes. Here's the energy level diagram for the ion. The upward brown arrows show the possible excitations due to the incoming electron. The downward arrows show the possible transitions for which a photon could be emitted.

 

[CFXMSC]

I got it! Thank you TSny. The final step is solve the equation 2.

 

[TSny]

Good!