Physics Experiment: Jerk & Inertia | Solving for dA/dt

[Pax]

There is this experiment my high school teacher showed in physics class. You are probably aware of it

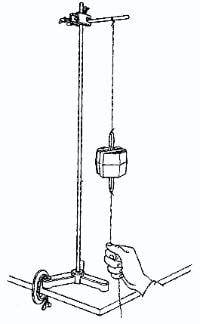(from practicalphysics.org)

There is a video of a teacher actually doing the experiment here:
https://sites.google.com/site/haatscience/physics/221-the-effect-of-inertia

Gradually pull the thread and the top thread breaks, jerk the thread and the bottom one breaks.

I tried to set up a free body diagram to show how this works, and most specifically to solve for the rate of change of acceleration (jerk) that will be the threshold between the top string breaking and the bottom.

I am at a loss, how do you put dA/dt into the equations?

Any ideas?

 

[Charles Link]

This one seems to be an experiment where you could model it as a tension that is applied. With a sudden jerk, the tension in the bottom string could be modeled as a delta function: $T_1(t)=T_{10} \delta (t)$. Because much of this is absorbed by the acceleration of the mass, the tension in the top string $T_2$ never reaches anywhere near the large value, basically infinite, of the $T_1(t)$ with its delta function. $\\$ (In principle, you could limit $T_1(t)$ to a finite value, by using some other function with characteristics similar to a delta function. For what gets transferred to the mass with a quick jerk, it is basically the impulse which is the integral $I=\int T_1(t) \, dt$).$\\$ Meanwhile, elasticity equations are needed for the top string: $T_2=k (x-L)$ where $x$ is the position of the mass $M$ (with origin $x=0$ at the top position of the attachment of the string), and $L$ is the length of the string with no mass attached. $\\$ The mass $M$ has $Mg+T_ 1-T_2=M \ddot{x}=Mg+T_{10} \delta(t)-k(x-L)$ , with initial conditions that $Mg= k(x_o-L)$. $\\$ You can solve for $x(t)$ , and then for $T_2(t)=k(x-L)$. $\\$ Anyway, I haven't solved these equations, but I think they would give the necessary result. $\\$ Edit, along with a correction to my first attempt at a solution here: $\\$ I get for $t \leq 0$, that $x(t)= \frac{Mg}{k}+L$, and $T_2(t)=Mg$ , $\\$ and for $t>0$, an impulse has been added to the mass $M$, giving it an initial velocity, but no immediate change in position occurs. After that mass $M$ performs simple harmonic motion with this energy that it has acquired. You can compute the maximum $x$ that occurs in the simple harmonic motion, and thereby compute $T_{2 \, max}=k (x_{max}-L)$. I get, with a quick calculation, that the simple harmonic motion (at frequency $\omega=\sqrt{\frac{k}{M}}$ ) has amplitude $\frac{T_{10}}{\sqrt{kM}}$, so that $\\$ $x_{max}-L=\frac{T_{10}}{\sqrt{kM}} +\frac{Mg}{k}$, and that $T_{2 \, max}=T_{10} \sqrt{ \frac{k}{M}}+Mg$. $\\$ For most cases, with a quick jerk, $T_{2 \, max} <<T_{1 \, max}$. $\\$ Meanwhile, with a steady pull on $T_1$ the tension $T_2=T_1+Mg$, and $T_2$ (the tension in the upper string) is larger and the upper string breaks.