Physics Wordy Question: Calculating Areas and Masses on a Graph - Help Needed!

[farhana21]

Can someone please help me on this question please.

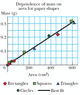
A student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. He cuts out various shapes in various sizes, calculates their areas, measures their masses and prepares the graph in the figure below.

(a) Consider the fourth experimental point from the top. How far is it from the best-fit straight line? Express your answer as a difference in vertical-axis coordinate.

The answer for part a is 0.015g

(b) Express your answer as a percentage.
(c) Calculate the slope of the line.

I need help on part b and c of this question.

The answer for part b is not 1.5% i already tried this.


I have attached a graph for you all to look at.

Thanks for the help and assistance in advance.

Its much appreciated

 

[Simon Bridge]

(b) You don't know how to work out a percentage?

The answer for part b is not 1.5% i already tried this.

- you have to say what you tried!

The trick is to figure out what the number is supposed to be a percentage of.
Divide the number by what it is supposed to be a percentage of, then multiply the result by 100.

if the value is y and the deviation is Δy, then "Δy is 100*Δy/y percent of the value".

(c) to work out the slope of the line, find the coordinates of two points on the line (any two that are not data points: read them off the graph). The equation of the line that goes through both of them is y=mx+c, m is the slope. m=Δy/Δx

 

[farhana21]

The answer for part c is The answer to part c is 0.00052 g/cm^3

would someone please kindly tell me the answer to part b.

im really stuck.

help is most appreciated

Thank you

 

[Simon Bridge]

would someone please kindly tell me the answer to part b.

Er... nope: that would be against the rules.

What is the difficulty with part (b)?
Check your working for part (c).

I cannot help you if you don't show me your working.

 

[farhana21]

For part (c) I chose a grid point on the line far from the origin: slope = 0.31 g/600 cm2 = 0.000 52

For part (b) I did (200, 0.1) (300, 0.15).

Then (0.15-0.1)/(300-200) = 5* 10^-4 * 100 *100 = 5%

 

[mfb]

For part (c) I chose a grid point on the line far from the origin: slope = 0.31 g/600 cm2 = 0.000 52

Ok, but your units are wrong.

For part (b) I did (200, 0.1) (300, 0.15).

Then (0.15-0.1)/(300-200) = 5* 10^-4 * 100 *100 = 5%

How is that related to (a)? You should give the absolute deviation calculated in (a) (0.015g) as relative deviation.

 

[Simon Bridge]

I would add:

For part (b) I did (200, 0.1) (300, 0.15).
Then (0.15-0.1)/(300-200) = 5* 10^-4 * 100 *100 = 5%

That looks like the slope of a line between the two points names expressed as a percentage. What were you are asked to find again?

For part (c) I chose a grid point on the line far from the origin: slope = 0.31 g/600 cm2 = 0.000 52[units?]

... that works provided the line passes through (0,0) - it aught to, since zero area implies no material - assuming that nothing unanticipated is going on.

Statistical or systematic errors could lead the actual data to produce a line that does not go through zero. Taking the slope through two points would reveal this.

Some courses like students to fudge results like this though.