Solving Pinned Jointed Frame Exterior Reactions

[matthew_hanco]

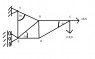
The problem is attached to this post, basically i need the exterior reactions and how to work them out.

i know i need to take moments I am just not sure how to work it out.


Basically what i worked out

is

i assumed horizontal members are equally to 1

sum of the horizontal = 0 5Kn- HA - HE=0

Sum of the vertical =0 10KN- VA =0

But that is where I am stuck i know the numbers should be roughly

HA=20
VA= 10
HE = 15

But i know it is more accurate than that I am not sure if i need to include sine or cosine in the solution

Thanx in advance

 

[matthew_hanco]

To add to it i have just tried

sum MA= 0

Therefore he x 2 - 5x1 - 10x2 =0

he =12.5

sum of horizontal 5+12.5 =17.5

therefore ha = -17.5

sum of the vertical

Va -10 x 1 =0

so Va = 10

Is that right?

 

[matthew_hanco]

Im desperate and really need someones help urgently.

 

[Q_Goest]

sum MA= 0

Therefore he x 2 - 5x1 - 10x2 =0

he =12.5

Hi matthew,
Since you're taking moments around A and since the 5 kn and 10 kn forces produce opposite moments around A, one of your terms needs to be positive and one needs to be negative. You have a negative moment around A for BOTH of these forces.

Once you get the horizontal force from E you can sum forces and get the horizontal and vertical forces on A.

 

[matthew_hanco]

ok so the new calculated resultant forces would be

He= 15 ( (-10 x 2) - (+5x1) + He=0)

Ha= -20 (+15 + 5 - ha= 0 therefore Ha= -20)

Va= -10 (+10 -Va=0)


But now checking my lecturers answers he gives

14.82 for He

And a resultant force for a 22.2 acting 26.46 degrees from the horizontal


But with my results the resultant for a is 22.36 and 26.56 from the horizontal.

who is right, if he is how can i account for the discrepencies

 

[Q_Goest]

Those answers are all pretty close, so I would guess the differences are in rounding error. Regardless, I can't check the math because the figure you provide has no dimensions on it.

 

[matthew_hanco]

All forces are in KN

 

[Q_Goest]

I can see the forces. There are no linear dimensions on your picture.

 

[nvn]

matthew_hanco: The dimensions are already fully defined by the diagram given in post 1. The resultant reaction force at point A from your lecturer, 22.20 kN, is correct. However, the orientation angles given by both you and your lecturer are currently incorrect. The resultant reaction force at point A is 22.20 kN acting 26.77 deg from the horizontal. Keep trying. Your discrepancies are not due to round-off error. First, figure out the correct dimensions of your structure, and label them on your free-body diagram. You currently appear to be using wrong dimensions.

 

[matthew_hanco]

Got it, the length should be root 3 instead of 1.

so it should be

(-10 x (root3x2) - +5x1)/2=Ha

 

[nvn]

Excellent, matthew_hanco.