Please Can someone check my answer, ITS DONE, needs checking.

[livestrong136]

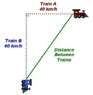
1. Two trains start from the same point at the same time, one going east at a rate of 40 km/h and the other going south at 60 km/h, as shown in the diagram at right. Find the rate at which they are separating after a) 1 h of travel b) 2 h of travel. You must show how to find the answer using calculus. (DIAGRAM IS ATTACHED)

a² +b² = c²
40² + 60² = c²
√4̅0̅²̅ ̅+̅ ̅6̅0̅²̅ = c
c = 72.11 km/h

MY TEACHER SAID THIS, SHE TOOK OFF 4 MARKS: "you cannot just use pythagorean theorem, you must take the derivative of the pythagorean theorem function and then find s'(1) to find the rate of separation. You did not show all of your work and it doesn't show your understanding." (-4 marks)

SO NOW I DID IT THIS WAY?

D = √A^2 + B^2

Using A = 40t and B = 60t to represent the distances with respect to time, we get

D(t) = √(40t)^2 + (60t)^2 = √1600t^2 + 3600t^2 = √5200t^2

D't= 10,400t/2√5200t^2 = 5200t/√5200t^2

After 1 hr
D' (1)= 5200(1)/√5200(1)^2 = √5200 = 72.1 km/h

Is This way better? I mean is it this that my teacher wants me to do? SO that means to get the answer for b (2 hrs), DO I SUB IN THE 2 in the very last step?

 

[LCKurtz]

Yes the second way is better. Why not simplify it more:$$
D'(t) = \frac{5200t}{\sqrt{5200t^2}}=\sqrt{5200}$$This tells you that the rate at which they are separating doesn't depend on $t$ so you get the same answer when $t=2$.

You just got lucky getting the correct answer the first way. That "method" is completely incorrect. Not to mention that the problem instructions said you must use calculus for your method.