jayanthd
- 16
- 0
Please see the attached image. There are 6 figures.
Please explain the proofs for sin(90 - θ) w.r.t the 2nd, 3rd and 4th images. I understand the proof w.r.t 1st image.
In the 2nd image y1 and x is negative. In 3rd image y, y1, x, x1 are all negative and in the 4th image y and x1 are negative. How he gets +ve value for sin(90 - θ) w.r.t 2nd, 3rd and 4th figures?
In the 3rd fig. -y1 = -x and -y = -x1.
-y1/r1 = -x/r = -cos(θ)
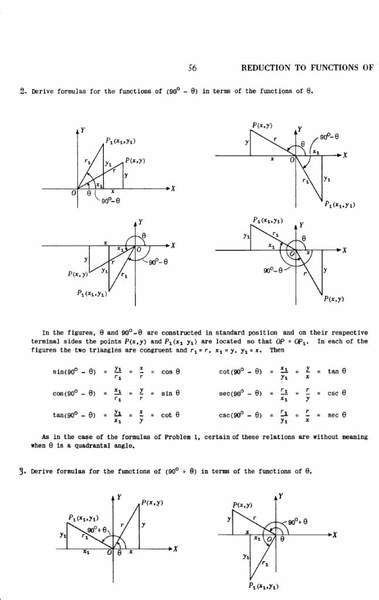
Please explain the proofs for sin(90 - θ) w.r.t the 2nd, 3rd and 4th images. I understand the proof w.r.t 1st image.
In the 2nd image y1 and x is negative. In 3rd image y, y1, x, x1 are all negative and in the 4th image y and x1 are negative. How he gets +ve value for sin(90 - θ) w.r.t 2nd, 3rd and 4th figures?
In the 3rd fig. -y1 = -x and -y = -x1.
-y1/r1 = -x/r = -cos(θ)

