Point rotating in a coordinate system

[Karol]

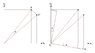
The point P rotates with angle α to point P'. the coordinates of the old P are x₁ and x₂ and for P': x'₁ and x'₂.
Prove that:
$$x'_1=x_1\cos\alpha+x_2\sin\alpha$$
$$x'_2=x_2\cos\alpha-x_1\cos\alpha$$

I drew on the left the problem and on the right my attempt. the line OA, which is made of $x_1\cos\alpha$ plus $x_2\sin\alpha$ which is the blue line is indeed x'₁ but i don't see the congruent triangles.

 

[RyanH42]

$P(x_1,x_2)$ and If we rotate α degree we get new coordinates $P'(x'_1,x'_2)$.Now Let make a vector which initial point Origin and terminal point P.This vector has magnitude R.Now we can show this vector in like this P=R(cosβ+sinβ) so $x_1=Rcosβ$ and $x_2=Rsinβ$.Now we want to rotate this coordinate α degree.

This will lead us $x'_1=Rcos(β+α)$
and $x'_2=Rsin(β+α)$.Think this way.

 

[Karol]

Thanks RyanH, i solved