Position of Block on Incline w/ & w/o Friction

[ksle82]

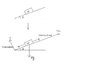
Find the position of the block as a function of time for both cases:
a)friction
b)frictionless

Here're my answers. Please check to see if they're correct. The free body diagram are attached.

https://www.physicsforums.com/attachment.php?attachmentid=7068&stc=1&d=1149476915
slidingblock.JPG

a) x(t)= .5g(cos(theta)-sin(theta))t^2
b) x(t)= .5gsin(theta)t^2

 

[arunbg]

Although I can't see your attachments , where's the coefficient of kinetic friction in the first part of the question ?
Also is your X-axis along the incline ?

 

[ksle82]

Although I can't see your attachments , where's the coefficient of kinetic friction in the first part of the question ?
Also is your X-axis along the incline ?

coefficient of friction is not given, so i just assume it's mu (u). i don't know if one can do this or not. But if one has to calculate it, u is usually tan(theta).


And yes, x-axis is along the incline.

 

[Doc Al]

coefficient of friction is not given, so i just assume it's mu (u). i don't know if one can do this or not. But if one has to calculate it, u is usually tan(theta).

That's not true, in general. What you are probably thinking of is the relationship between the coefficient of static friction (between an object and a surface) and the (special) angle at which the object just begins to slide. For that specific angle, \mu_s = \tan\theta.

But what you what is the coefficient of kinetic (sliding) friction, assuming the object starts from almost rest. What's the exact statement of the problem?

Your free body diagram looks OK to me.