Possible new formula for simple tension problems

  • Thread starter Thread starter Soenhay
  • Start date Start date
  • Tags Tags
    Formula Tension
AI Thread Summary
A new formula for solving simple tension problems involving a weight suspended by two cables with tensions T1 and T2 and angles A and B has been proposed. The formula aims to provide a quicker solution to these types of problems, although some participants believe it may not be particularly innovative or useful. The discussion includes a proof that illustrates the potential time savings when applying this formula. Overall, the community encourages exploration of new approaches in physics problem-solving. This formula could offer a fresh perspective on tension calculations.
Soenhay
Messages
1
Reaction score
0
A quick shortcut for problems that involve a weight (W) hanging from two cables with tensions T1 and T2 and angles A and B.

Probably not that useful.
Probably already known.

But just in case here it is:


Formula_7_6_2011_scaledown.png



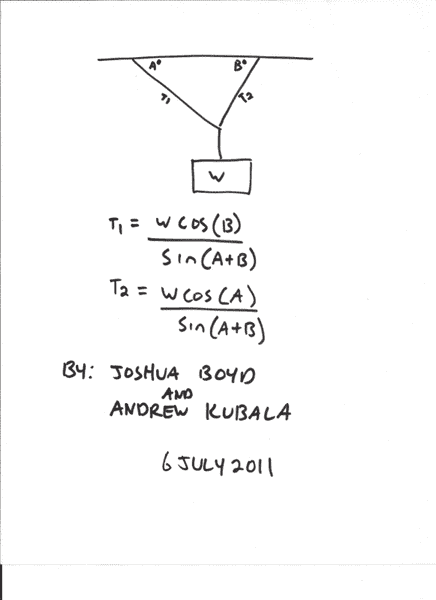
The following is the proof which also shows how much time one might save:


Proof_7_6_2011_scaledown.png
 
Physics news on Phys.org
Hello Soenhay and welcome to Physics Forums.

That's a neat little formula, I don't think I've seen it put that way before so keep at it you never know what you might come up with next.

:smile:
 

Thread 'Is calling fictitious forces "not real" just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

I Understanding tension and centripedal force in a puck and weight
Replies
4
Views
2K
Problem involving space elevators
Replies
19
Views
2K
Tension in a deformed cylindrical bag on a surface
Replies
18
Views
1K
Cosine, Sin, Tangent when find force/tension
Replies
3
Views
13K
I Forces and gravitational time dilation
Replies
11
Views
2K
Don't Understand Tension in this Instance
Replies
1
Views
1K
Basic torque/static equilibrium problem
Replies
12
Views
3K
Analysis of Forces Acting at Knot in Tension Rope Figure
Replies
13
Views
10K
Tension of cables of unequal length
Replies
2
Views
2K
Adjustable spring tensioner for 90deg rotating arm
Replies
5
Views
3K

Hot Threads

Recent Insights

Back
Top