Lauren1234
- 26
- 3
- Homework Statement
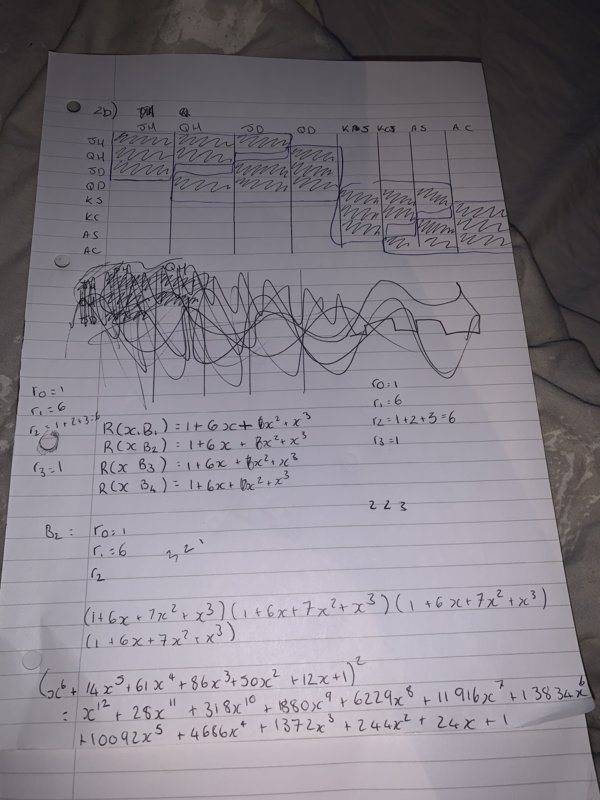
- both the type and the suit of the card are important. Each pack again consists of eight cards; the Jack and Queen of Hearts and Diamonds, and the King and Ace of Spades and Clubs. A ‘snap’ occurs when two cards that are either of the same type OR suit appear together. Find the total number of possible orderings of the cards which result in no snaps. (You may first wish to assume that the order of the cards in the first pack is fixed.)
- Relevant Equations
- Below
This is my solution however I feel like the number is far too big can anyone see what I’ve done wrong