Potentetiometer - position of slider

[damon669]

Homework Statement

https://www.physicsforums.com/attachment.php?attachmentid=60570&stc=1&d=1375128608
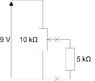
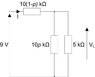
Thew circuit shows a 10KΩ potentiometer with a 5KΩ load. determine the position of the slider on the 'pot' when tthe voltage across points 'XX' is 3V

Homework Equations

The Attempt at a Solution

Vi=IR
I=V/R = 12/10x10^3 = 0.0012A = 1.2mA
Vo=IR
I=Vo/Io = 3/5x10^3 = 0.0006A = 0.6mA
Vi/Ri+Ro = 9/10x10^3 + 5x10^3 = 0.6mA
VD Across Ri =Vi =RiVi/Ri+Ro = RiVi/R

 

[rude man]

?
Let x = fraction of distance from ground to wiper.
Call the potentiometer resistance (10K) = R1 and the external resistor (5K) = R2.
Call 9V = Vi and wiper voltage = Vo = 3V.
Then redraw your circuit so that Vo/Vi consists of a voltage divider between two equivalent resistors.
What is the equivalent resistor going from Vi to Vo?
What is the equivalent resistor going from Vo to ground?
Solve for x.

 

[damon669]

Do you mean like this

https://www.physicsforums.com/attachment.php?attachmentid=60665&stc=1&d=1375517436

 

[mfb]

Do you mean like this

https://www.physicsforums.com/attachment.php?attachmentid=60665&stc=1&d=1375517436

No, that is the equivalent circuit if the slider is in the top position.

A potentiometer is similar to two resistors in series, where the slider gives a connection to the connection between those two resistances. In addition, you can adjust those two resistances by moving the slider.

 

[damon669]

so something like this then

https://www.physicsforums.com/attachment.php?attachmentid=60681&stc=1&d=1375603969

 

[mfb]

That is right.
I would align the two resistors to be in the same column, but that is just a graphical thing and does not influence the electric properties.

 

[damon669]

so now to answer the question

I need to find the new parallel resistence which is (R_1 R_2)/(R_1+R_2 )
=33x10^3 ohms

Then I think I have to put 3 V in the equation?

 

[mfb]

The parallel resistance should depend on the position of the slider, and don't forget the third resistor in your analysis.
What do you mean with "put 3 V in the equation"? Just do it.

 

[rude man]

so now to answer the question

I need to find the new parallel resistence which is (R_1 R_2)/(R_1+R_2 )
=33x10^3 ohms

Then I think I have to put 3 V in the equation?

Your diagram is correct. But the parallel resistance is obviously a function of p.

yes, put 3V at the output and solve the whole thing for p.

 

[damon669]

I think somebody needs to get the glove puppets out :)

 

[damon669]

Vl=RoVi/R1+R2

3=Ro•9/(10•10^3)+(5•10^3)

= 5k ohms

 

[mfb]

I don't understand where that formula comes from. And where did you define all those parameters?

 

[damon669]

Vl = 3 volts across the load
Ro = what I'm trying to find
Vi = voltage on the circuit
R1 = 10k ohms
R2 = 5k ohms

 

[damon669]

That formula came from my notes

 

[damon669]

voltage division.

is it correct then?

 

[mfb]

R1 = 10k ohms

There is no 10kOhm-resistor in your network.

That formula came from my notes

It should come together with a circuit where you can apply it. You cannot just use a formula for some circuit here.

 

[damon669]

10k ohm is the max position of the slider @ 9V

 

[mfb]

Sure, but 10kOhm is not a single resistor in your network.
The maximal position of your slider is not the solution to this problem.

 

[damon669]

If the slider was at 5k ohm would that not give 3 volts across the load?

 

[mfb]

It would, but I think it is an accident that the formula gives the right result.
Try to do the same calculation for 0V, 9V and 4V, and see what you get (and show what you plugged in where please). Are the results reasonable?

 

[damon669]

Can this be done without using a Quadratic equation?

 

[rude man]

No, but it's a piece of cake - especially if you use Wolfram Alpha!

 

[damon669]

so you DO have to use a Quadratic to solve then

 

[rude man]

so you DO have to use a Quadratic to solve then

Yes.

 

[damon669]

OK this is what i got then

Let p represent the position of the ‘pot’ slider where 0≤p≤1 (i.e. the proportion of the ‘pot’ resistance that is in parallel with the load resistor). For p=0 the slider is at the bottom (minimum resistance) and for p=1 the slider is at the top (maximum resistance). The equivalent circuit is shown below.


The parallel resistance R_P is given by

R_P=(10p×5)/(10p+5) kΩ

=50p/(10p+5) kΩ

=10p/(2p+1) kΩ

and the current I is given by

I=9/〖10(1-p)+R〗_P
=9/(10(1-p)+R_P ) mA

 
The voltage V_L across R_P is

V_L=I×R_P

=(9R_P)/(10(1-p)+R_P )

=(9×10p)/(10(1-p)(2p+1)+10p)

Now V_L=3 so

3=(9×10p)/(10(1-p)(2p+1)+10p)

3=9p/((1-p)(2p+1)+p)

(1-p)(2p+1)+p=3p

2p+1-2p^2-p+p=3p

0=2p^2+p-1

Therefore,
p=(-1±√(1-2(2)(-1) ))/(2×2)

=(-1±√9)/4

=(-1±3)/4

Since 0≤p≤1 then p=0.5. Thus the slider is at the midpoint position of the ‘pot’.
Check: R_P=2.5 kΩ which is in series with a resistance of 5 kΩ so the voltage V_L across the load is

V_L=(9×2.5)/(2.5+5)

=3 V

 

[rude man]

Looking good. I didn't check all your math but you have the right approach & the answer is of course correct also.