scef333
- 3
- 0
Potential of Concentric Cylindrical Insulator and Conducting Shell...Please Help
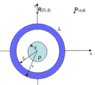
An infinitely long solid insulating cylinder of radius a = 3.6 cm is positioned with its symmetry axis along the z-axis as shown. The cylinder is uniformly charged with a charge density ρ = 40 μC/m3. Concentric with the cylinder is a cylindrical conducting shell of inner radius b = 18.9 cm, and outer radius c = 23.9 cm. The conducting shell has a linear charge density λ = -0.4μC/m. An infinitely long solid insulating cylinder of radius a = 3.6 cm is positioned with its symmetry axis along the z-axis as shown. The cylinder is uniformly charged with a charge density ρ = 40 μC/m3. Concentric with the cylinder is a cylindrical conducting shell of inner radius b = 18.9 cm, and outer radius c = 23.9 cm. The conducting shell has a linear charge density λ = -0.4μC/m.
What is Ey(R), the y-component of the electric field at point R, located a distance d = 58 cm from the origin along the y-axis as shown?
What is V(P) – V(R), the potential difference between points P and R? Point P is located at (x,y) = (58 cm, 58 cm).
What is V(c) - V(a), the potentital difference between the outer surface of the conductor and the outer surface of the insulator?
I'm having trouble converting the charge density ρ = 40 μC/m3 and λ = -0.4μC/m to Q in order to find the electric field at point R due to the insulating and conducting cylinders. Please let me know what you think. There is a diagram attached.
Homework Statement
An infinitely long solid insulating cylinder of radius a = 3.6 cm is positioned with its symmetry axis along the z-axis as shown. The cylinder is uniformly charged with a charge density ρ = 40 μC/m3. Concentric with the cylinder is a cylindrical conducting shell of inner radius b = 18.9 cm, and outer radius c = 23.9 cm. The conducting shell has a linear charge density λ = -0.4μC/m. An infinitely long solid insulating cylinder of radius a = 3.6 cm is positioned with its symmetry axis along the z-axis as shown. The cylinder is uniformly charged with a charge density ρ = 40 μC/m3. Concentric with the cylinder is a cylindrical conducting shell of inner radius b = 18.9 cm, and outer radius c = 23.9 cm. The conducting shell has a linear charge density λ = -0.4μC/m.
Homework Equations
What is Ey(R), the y-component of the electric field at point R, located a distance d = 58 cm from the origin along the y-axis as shown?
What is V(P) – V(R), the potential difference between points P and R? Point P is located at (x,y) = (58 cm, 58 cm).
What is V(c) - V(a), the potentital difference between the outer surface of the conductor and the outer surface of the insulator?
The Attempt at a Solution
I'm having trouble converting the charge density ρ = 40 μC/m3 and λ = -0.4μC/m to Q in order to find the electric field at point R due to the insulating and conducting cylinders. Please let me know what you think. There is a diagram attached.