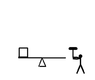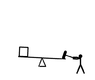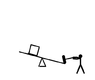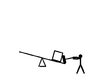- #1
adjacent
Gold Member
- 1,552
- 63
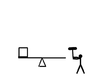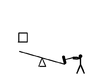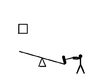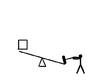
In the image a man hits the plank with that hammer with the same force for 2second
Another man hits it in the same manner for 10seconds.In the first round the box rises up.In the second round however,it does not rise.I know that the power is greater in the first round but does not know why it rises. I also know that
P=(FS)/t
P=FV
P=Energy transferred/time taken
Another man hits it in the same manner for 10seconds.In the first round the box rises up.In the second round however,it does not rise.I know that the power is greater in the first round but does not know why it rises. I also know that
P=(FS)/t
P=FV
P=Energy transferred/time taken