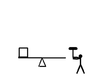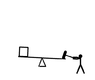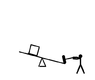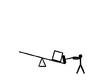Power & Velocity: Physics Explained

[adjacent]

In the image a man hits the plank with that hammer with the same force for 2second
Another man hits it in the same manner for 10seconds.In the first round the box rises up.In the second round however,it does not rise.I know that the power is greater in the first round but does not know why it rises. I also know that
P=(FS)/t
P=FV
P=Energy transferred/time taken

 

[Simon Bridge]

I think the question will need some clarification before it can be properly tackled.

A force F is applied for time T to the end of a lever - equal distance on the other side of the pivot in a mass m.
The mass is observed to rise ... suggesting that F > mg.

If the experiment is repeated with the same force F for time 2T (i.e. twice as long) then the mass should still rise since F > mg still. It should, in fact, rise further.

So I don't think you have described the situation you are thinking of.

Notes
- the force of a hammer blow usually has a quadratic dependence on time. F(t)=F_{max}(T-t)t
- if you think of it in terms of energy transfer - then a lower power means the energy is transferred slower, and so the mass raises slower, is all.

 

[adjacent]

I think the question will need some clarification before it can be properly tackled.

A force F is applied for time T to the end of a lever - equal distance on the other side of the pivot in a mass m.
The mass is observed to rise ... suggesting that F > mg.

If the experiment is repeated with the same force F for time 2T (i.e. twice as long) then the mass should still rise since F > mg still. It should, in fact, rise further.

So I don't think you have described the situation you are thinking of.

You are wrong.The same amount of work is done if I apply the same force for the same distance(Of the lever_vertical distance)If I do the work for a greater time,the power is less.Then why should it rise much further.Please explain

 

[tiny-tim]

I think the question will need some clarification before it can be properly tackled.

i agree

where does this question come from? what is the full question?

 

[adjacent]

i agree

where does this question come from? what is the full question?

I presented the question.Simon bridge presented it much clearly.Can you answer to my doubt on #3?

Actually the question is:Someone applies a force on the lever for 2 sec.The box rises up.Again anotherone applies the same force as first on for 10 sec.This time the box does not rise(Rise meaning leave the lever and rise up and fall).Why is that?

 

[Simon Bridge]

You are wrong. The same amount of work is done if I apply the same force for the same distance (Of the lever_vertical distance) If I do the work for a greater time,the power is less.

You meant that the same work was to be done each time ... but the second time, the work is done over a longer period?

Then why should it rise much further. Please explain

It wouldn't.

Regardless of the amount of time the work took place in, with no other losses, you get the same change in energy of the system. This means that, in each experiment, the mass is elevated the same vertical distance h: h=W/mg

In my response (post #2), you have read that I had the same constant force being applied for a longer time - which means that more work is done, so the distance lifted is greater.

You should be able to do the kinematics to figure it out.

Your original question (post #1) says there was movement the first time but none the second time - which means that the work was not the same in both instances.

This means that your question is incomplete.

 

[adjacent]

You meant that the same work was to be done each time ... but the second time, the work is done over a longer period?
It wouldn't.

Regardless of the amount of time the work took place in, with no other losses, you get the same change in energy of the system. This means that, in each experiment, the mass is elevated the same vertical distance h: h=W/mg

In my response (post #2), you have read that I had the same constant force being applied for a longer time - which means that more work is done, so the distance lifted is greater.

You should be able to do the kinematics to figure it out.

Your original question (post #1) says there was movement the first time but none the second time - which means that the work was not the same in both instances.

This means that your question is incomplete.

Power is also Force*Velocity,Meaning if the power is greater (and the same force applied)the velocity should be greater too which means at the first time (Force applied for two sec, the power was greater),the box will rise up.Why is this wrong?

 

[adjacent]

I will give a gif image

 

[adjacent]

Assume in the two pictures the lever(side closer to stickman)covered the same distance.He used the same force(The box had 10N).So the same work is done.But at the first time(First image)he applied that force for a longer time the box did not rise.In the second image he applied the force for a short time,the box rises.Why? (Watch it.Its GIF)
Note:This if fictional but it happens the same in real life too

 

[Dale]

Assume in the two pictures the lever(side closer to stickman)covered the same distance.He used the same force.So the same work is done.But at the first time(First image)he applied that force for a longer time the box did not rise.In the second image he applied the force for a short time,the box rises.Why? (Watch it.Its GIF)
Note:This if fictional but it happens the same in real life too

The part in red is wrong (which leads to other mistakes). You cannot get these two different results if the force is the same. If you apply a force to the same object for a shorter time over the same distance then the force must be greater, not equal.

 

[adjacent]

If you apply a force to the same object for a shorter time over the same distance then the force must be greater, not equal.

Can you explain your answer and give me an equation which relates force,time and distance.(Power equation can be used but we don't know the power-So please explain

I Want The Entire Explanation For This

 

[Dale]

Can you explain your answer and give me an equation which relates force,time and distance.(Power equation can be used but we don't know the power-So please explain

Are you familiar with SUVAT? Take the second SUVAT equation, and set u=0, and solve for a. That gives you acceleration as a function of time and distance. Then substitute in Newton's second law to get force as a function of time and distance.

What formula do you get? As time decreases what happens to force according to that formula?

 

[Simon Bridge]

Ah I see ... if you strike a sharp blow, the mass is thrown into the air, while a slow blow just lifts the mass without the mass leaving the lever.

In the second gif, the amount of work done is much less than in the first one.
You can tell because the mass does not rise as high as in the first gif.
This is important!

What is happening:
1. Energy is transferred from the hammer to the lever+mass as rotational kinetic energy+gravitational potential energy.

2. When the force stops, the lever+mass should still keep rotating ... now only gravity is acting on it and the kinetic energy in the lever+mass system is exchanged for gravitational potential energy.

3. The lever+mass system rotates until all kinetic energy is exchanged for gravitational potential.

Looking at the first gif, where the box leaps into the air... what is stopping the rotation of the lever?
What must have happened is the lever hit something that stopped it - probably the hammer-end hit some surface like the ground? That's important!

The lever has been prevented from rotating while the box still has some kinetic energy left It is no longer pushed around by the lever - so it should continue, by the law of inertia, at a tangent to the circular motion. In your gif, the box goes straight up when it should go at an angle towards the hammer-wielder - and it should continue in a ballistic arc.

In the second gif, where the box does not get thrown in the air, you have the lever rotating the same amount as in the first one. This means the hammer falls through the same distance as in the first one ... but it takes longer. Same distance in more time means smaller acceleration, smaller acceleration (by F=ma) means less force.The situation you have depicted looks a bit like a carnvival strength tester where peple are invited to strike a short lever with a hammer to see how high a weight will go off the other end.
Like this:

... you'll see that the man demonstrating first does a slow push, and the weight does not fly up - then he does a quick one and the weight flies up - but the second time he uses a lot more force as well.

 

[sophiecentaur]

I think a different approach may help to explain the situation - based on Momentum. Read this before rejecting it out of hand. The point is that loads of energy is actually wasted during this process so you can't base any calculations on Energy In = Useful Energy Out. (this is the basic difficulty)

The OP describes the change in Momentum because the Impulse (Force times time) is how the problem is posed. This is a similar problem to that of launching a rocket, in which there is a constant flow of ejecta causing acceleration due to a series of impulses. We are presumably assuming that there is no 'ratchet', so the lever can fall back down again if the next hammer blow is not enough or the delay is too great.
This is, again, just like the rocket on the launchpad, which requires a certain minimum power in order to lift the payload at all.

So the rate of change of momentum (the load mass (M) times the acceleration) must be greater than Mg for the lever to keep moving the mass upwards. The change in momentum is provided by a series of impulses from the hammer (mass m and velocity v) at a rate f hits per second.
So mvf > Mg for the mass to rise due to the hammering.
If it does rise, the initial acceleration (a) will be in the equation

Ma = mvf - Mg

The actual energy transferred to the rising mass will very with time (as with a rocket) and the initial amount of energy is small but increases with time - rocket engines are actually zero efficient at the start of the launch.

The Kinetic Energy of the Mass will be M(v')²/2 where v' is the instantaneous velocity of the rising Mass and
v' = at

I think this will give you the answer you want.

 

[Simon Bridge]

I was thinking that a picture could help...

https://www.physicsforums.com/attachment.php?attachmentid=59224&stc=1&d=1370226389​

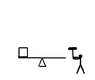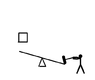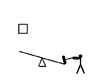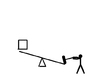
(above) the head of the hammer is mass M, it starts out height h above the ground as the player puts their effort into bringing it down.

The player, here, adopts a strategy of raising the hammer as high as possible and bringing it down as straight as they can - so the trajectory of the hammer-head (light green) is not going to be circular. The hammer strikes the lever a time t₀, a distance r from the pivot - the lever moves through angle θ (which we will consider small enough to approximate sinθ≈θ and cosθ≈1 to keep the math simple) and strikes the ground at time t₁ where it stops turning.

The mass being lifted is m, a distance r on the other side of the lever to the hammer.
In this picture, I am constraining it to move vertically (vertical dotted line) only so I don't have to worry too much about friction.
The mass remains stationary until time t=t₀, when it starts to rise.
At t=t₁ it has risen through height y=y₁ and the lever stops pushing it up.
It continues, however, due to the law of inertia, until it reaches a final height y=y₂ at time t=t₂, where it starts to fall again.

We want to consider two situations
1. where y₂ > y₁
2. where y₂ = y₁

The assertion in post #1 and subsequently is that both these situations can be achieved using the same constant force from t0-t1, but for different lengths of time.

Hopefully this will be suitable for OPs discussion.

In the energy picture, the hammer delivers energy to the mass as W = Mgh + E where E is supplied by the muscles of the player. The mass is, therefore, able to rise a total of y₂ = W/mg.
If follows that for y₂ > y₁ the work supplied must be greater ... but, if a constant force has been applied both times, then the work is the same, and this cannot have happened. This is the contradiction that so confuses Adjacent (OP).

The answer, of course, is that the same force cannot have been applied both times.
The contradiction proves it.

@Adjacent: you should do the math.

Real life hammer blows are quite complicated.
Lets forget the hammer for a bit and just say there is some mechanism that acts to provide a constant force F where the hammer would otherwise strike, for a time period T = t₁ - t₀.

This force is delivered, via the lever, directly to the bottom of the mass m.
So the free body diagram for mass m for t₀ ≤ t < t₁ has two forces, and for t ≥ t₁ has one force.
ƩF =ma will get the acceleration for each time-period.

The suvat (or "kinematic") equations can be used to find the distance the mass moves in each time period.

A simpler situation will help you understand what is happening ... a force F applied to mass m for time T will produce an acceleration a=F/m

If the mass starts at rest so u=0, then you can work out the equation for the distance s traveled as a function of T and F. Do it.

In order to double the time to travel the same distance, what has to happen to the force?

 

[Simon Bridge]

@Adjacent: You keep referencing the power ... so I should add a note about this.

You appear to be thinking of P=Fv where the velocity is a constant.
That is not the case for the situation above.

In a general real-life hammer blow, the force is not a constant either.
For a constant force P(t)=Fv(t) and you get a constant acceleration, and the velocity is given by the suvat equations.

In the simple case, horizontal motion mass m force F etc. that I insist you work out (see bottom of last post), you should also work out the power in each case.

Also - if you do the same work, same constant force, but at a lower power, what happens to the final velocity?

 

[sophiecentaur]

A simpler situation will help you understand what is happening ... a force F applied to mass m for time T will produce an acceleration a=F/m

If the mass starts at rest so u=0, then you can work out the equation for the distance s traveled as a function of T and F. Do it.

In order to double the time to travel the same distance, what has to happen to the force?

But you cannot determine F in an impact with as little information as this. You have to work in terms of Impulse and Momentum change. People are always posting questions involving 'the Force of a collision'. These questions really have no meaning as they stand.

 

[Simon Bridge]

But you cannot determine F in an impact with as little information as this. You have to work in terms of Impulse and Momentum change. People are always posting questions involving 'the Force of a collision'. These questions really have no meaning as they stand.

That's why I opted for simplified situations that did not involve a collision ;)

Novices often use "common sense" ideas to try to ask questions in a technical subject - as a result it can be tricky to ascertain reasonable meaning from a technical standpoint. That's why we gently explore the question first isn't it?

To me the description in post #1 does not lend itself well to an impulse treatment since the hammer remains in contact with the lever for the entire motion and there is a human pushing down through the entire motion too. Certainly you get an initial impulse when the head first strikes the lever but after that it gets complicated and we have to model the person as well. I don't feel up to it.

So I thought I'd leave the impulse and change of momentum stuff to you, if you don't mind. The diagram should be helpful for this, while I tackled the misunderstandings in the terms that Adjacent was trying to use.

Between us we should make some headway.

 

[sophiecentaur]

That's why I opted for simplified situations that did not involve a collision ;)

Novices often use "common sense" ideas to try to ask questions in a technical subject - as a result it can be tricky to ascertain reasonable meaning from a technical standpoint. That's why we gently explore the question first isn't it?

To me the description in post #1 does not lend itself well to an impulse treatment since the hammer remains in contact with the lever for the entire motion and there is a human pushing down through the entire motion too. Certainly you get an initial impulse when the head first strikes the lever but after that it gets complicated and we have to model the person as well. I don't feel up to it.

So I thought I'd leave the impulse and change of momentum stuff to you, if you don't mind. The diagram should be helpful for this, while I tackled the misunderstandings in the terms that Adjacent was trying to use.

Between us we should make some headway.

Yes, it is too complex a question for a simple answer. The hammer (it's mass and momentum) is, of course, a necessary part of the question or you may, just as well be talking about 'pressing down' the lever with your hand. The whole point of the 'try your strength' machine is accumulating momentum for the hammer on the way down and then there's an impulse. What you do when the hammer is actually in contact with the pad is anyone's guess (contact time will be a few hundred ms rather than 2s). I just reckon it's important not to subscribe to the 'force of an impact' notion because it cannot yield any understanding of the basics of collisions and the Energy Transfer aspect is a total unknown without detailed information about elasticity modulus and internal losses. As I said before, there are so many questions on PF which talk in those terms and the questioner will leave with as little as they came unless they are 'put right' about how to tackle such problems. We get many questions about recent car accidents, injuries and general damage to objects which can never be answered - despite the fact that they questions seems to be very reasonable. "Common sense" actually doesn't make sense in this context - natural reactions are actually pretty mediaeval and pre-Galilean.
Your comment in the second post:

I think the question will need some clarification before it can be properly tackled.

says it all.

 

[Simon Bridge]

I think OP has shown a basic misunderstanding about work, power, force, velocity, and displacement here though - it should be worth clearing it up. Most of what I've been doing is, in fact, the case of just pressing on the lever rather than modelling the strength-tester machine. Remember - we haven't had any confirmation from OP that this is what was intended.

Once OP has got the simple relation, the plan is to go backwards through the steps if modelling the strength tester is what is desired. But he should leave with a better idea about setting up thought-experiments.

@Adjacent: any of this any use to you?

 

[sophiecentaur]

Yep. A bit of feedback from OP is needed.

 

[adjacent]

I have got the answer I needed.Thank you two

Also - if you do the same work, same constant force, but at a lower power, what happens to the final velocity?

But have another question arising from the quote:
You said before,that if the same distance is covered in relatively less time,the force is greater
That means the same amount of work(F*S)cannot be done in 2sec and 4sec
Time is 2sec,if something covers for example 200m,the force supplied to it is greater than force supplied when it moves that very distance in 4sec-Meaning F*S is not the same in two different times.It follows that same amount of work cannot be done in different times(eg:2sec & 4sec)

What is wrong in this?Is it right or wrong?

 

[sophiecentaur]

I have got the answer I needed.Thank you two

But have another question arising from the quote:
You said before,that if the same distance is covered in relatively less time,the force is greater
That means the same amount of work(F*S)cannot be done in 2sec and 4sec
Time is 2sec,if something covers for example 200m,the force supplied to it is greater than force supplied when it moves that very distance in 4sec-Meaning F*S is not the same in two different times.It follows that same amount of work cannot be done in different times(eg:2sec & 4sec)

What is wrong in this?Is it right or wrong?

You are 'right' in as far as you are demonstrating that your particular approach doesn't really give results for the physical example you are using. The definitions of Force, Work and Power are what they are but, as you can have no idea about the forces involved when a hammer lands, you can't use them to find out what will happen.
You can calculate the result of a force acting for a time on a mass - because you can tell the acceleration (which will be uniform if the force is not changing). There are millions of simple examples where this approach works. Try Your Strength Machines are not one of those examples.

 

[Simon Bridge]

For the simple examples:

To cover the same distance in less time you need a higher acceleration, which means a higher force, which means that the work cannot be the same.

You can do the same work in less time, but you will have moved the object a different distance.

I gave you a bunch of exercises - please do them, they will clear things up.

The hammer blow OTOH is quite complicated.

 

[adjacent]

For the simple examples:

To cover the same distance in less time you need a higher acceleration, which means a higher force, which means that the work cannot be the same.

You can do the same work in less time, but you will have moved the object a different distance.

I gave you a bunch of exercises - please do them, they will clear things up.

The hammer blow OTOH is quite complicated.

That hammer blow came in my dreams,anyway thanks Simon bridge,sophiecentaur and dalespam.You have cleared my misunderstandings about power,work and force

 

[Dale]

Sorry if this is too late to help, but I wasn't thinking in terms of an actual hammers with all of the complexities of force involved. I was just thinking of a constant force applied over the fixed distance over a varying amount of time.

As you saw earlier, as you reduce the time that increases the acceleration and therefore increases the force. Increased force over the same distance increases the energy. That energy gets converted to kinetic and then gravitational potential energy, which determines how high it goes.

A real hammer force will not be constant, I was just simplifying.