Preconditioned conjugate gradient method

In summary, the preconditioned conjugate gradient method is a numerical algorithm used to efficiently solve large systems of linear equations, particularly those that are symmetric and positive definite. It works by finding a sequence of conjugate directions that converge to the solution of the linear system, using an approximate inverse of the matrix as a preconditioner to improve convergence rate and reduce computational cost. The method is often more efficient and accurate than other methods for solving linear systems, and can handle large, sparse matrices. However, it may not converge for certain types of matrices and requires an appropriate preconditioner. The performance of the method is evaluated based on the number of iterations and computational time needed to reach a desired level of accuracy, which can vary depending on the matrix and precondition
  • #1
Simon666
93
0
Hi, I've gotten the conjugate gradient method to work for solving my matrix equation:

http://en.wikipedia.org/wiki/Conjugate_gradient_method

Right now I'm experimenting with the preconditioned version of it. For a certain preconditioner however I'm finding that

223e5149b9e87962a93e50123795acb0.png


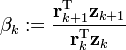
is zero, so no proper update is happening and hence no further minimizing of residuals occurs. Any idea what this means and what the best search direction (new p(k+1)) would then be?
 
Last edited by a moderator:
Mathematics news on Phys.org
  • #2
If ##\beta_k=0## then ##r_{k+1}=0## which is sufficiently small and the break criterion in the algorithm. I'd say you're done in this case.
 

FAQ: Preconditioned conjugate gradient method

1. What is the preconditioned conjugate gradient method?

The preconditioned conjugate gradient method is a numerical algorithm used to efficiently solve large systems of linear equations. It is particularly useful for solving linear systems that are symmetric and positive definite, which are common in many scientific and engineering applications.

2. How does the preconditioned conjugate gradient method work?

The method works by iteratively finding a sequence of conjugate directions that converge to the solution of the linear system. At each iteration, the method uses an approximate inverse of the matrix (known as a preconditioner) to improve the convergence rate and reduce the computational cost.

3. What are the advantages of using the preconditioned conjugate gradient method?

Compared to other methods for solving linear systems, the preconditioned conjugate gradient method is often more efficient and accurate. It also has the advantage of being able to handle large, sparse matrices, which are common in many real-world applications.

4. What are the limitations of the preconditioned conjugate gradient method?

The preconditioned conjugate gradient method may not converge for certain types of matrices, such as those with multiple eigenvalues that are close to zero. It also requires the user to choose an appropriate preconditioner, which can be challenging for some applications.

5. How is the performance of the preconditioned conjugate gradient method evaluated?

The performance of the method is typically evaluated based on the number of iterations required to reach a certain level of accuracy, as well as the total computational time. These metrics can vary depending on the matrix being solved and the choice of preconditioner.

Similar threads

Conjugate Gradient Methods Aren't Working
Replies
1
Views
2K
Steepest Descent Method with Matrices
Replies
1
Views
1K
I Gradient descent, hessian(E(W^T X)) = cov(X),Why mean=/=0?
Replies
4
Views
1K
Showing that the gradient of a scalar field is a covariant vector
Replies
5
Views
3K
Preconditioning the Steepest Descent Method
Replies
1
Views
2K
Conjugate gradient for nonsymmetric problem
Replies
4
Views
3K
Solving AX=B with Preconditioned Conjugate Gradient Algorithm
Replies
2
Views
4K
Optimization Solver - BFGS method with bound constraints
Replies
12
Views
12K
Efficient LSV Approximation for Large Matrices | Conjugate Gradient Method Guide
Replies
2
Views
2K
Is my math okay for gradient descent
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top