Preparing for Geometry/Algebra Test - Parametric Equations

[decibel]

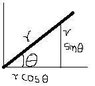
i have a geometry/algebra test tommorow and i have been sick for the whole unit, and my darn teacher is making me do it tommrow, even though i have no idea wuts going on...its on lines with parametric equations...if anyone has anything (tutorials, sites,etc.) anything that will help me understand it further, since the textbook is very hard to understand from...

thank you

 

[matrix_204]

parametric equations is the easy part of what ur learning.
a vector equation in the form (x,y,z)=(a,b,c)+t(A,B,C)
has parametric equation x=a+tA, y=b+tB, z=c+tC,
thats it, but i m pretty sure that this won't help u get good marks in ur test if u don't know n e thing else besides this.

 

[himanshu121]

I probably think u want answer in parametric form
as shown in diagram

x= r \cos\theta \\ y = r\sin\theta

by shifting the coordinate to x=x_1 and y= y_1
we get

The parametric equation is

\frac{x-x_1}{\cos\theta} = \frac{y-y_1}{\sin\theta} = r

Here x1, y1 is a fixed point on line and y,x req for equation
r being the distance between them