iki08
- 4
- 0
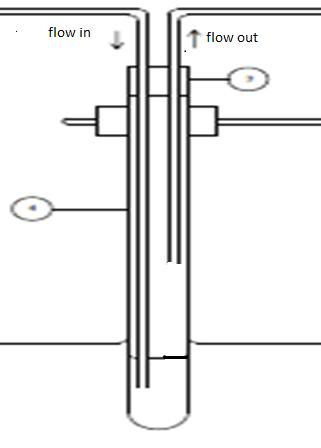
lets say if i have a test tube (diameter 3cm and height 30cm) seal with a rubber. in the test tube there 100ml of water = around 10 cm height. if air was flow into the test tube with flow rate around 20L/min, and after a few sec, the rubber was push out. in general i understand that the pressure inside the test tube is higher than atmospheric pressure. but i can't find any mathematical solution that relate flow rate and pressure to proof that the pressure inside the test tube is higher than outside. can anyone explain it to me.
Last edited: