Pressure regulator model: how to study its stability

[serbring]

Hi all,

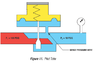
I need a model of a pneumatic pressure regulator. The model should be as simplest as possible and use an optimization solver to identify the regulator parameters in order to fit the performance I find in the datasheet of a commercial pressure regulator. I have already done a model using simpscape and I guessed the regulator parameters. In this condition the system is stable and it works as expected. When I run the optimization routine, the solver changes slightly the parameters and the system is not stable anymore, so the solver doesn't understand how to optimize the cost fuction. The model is non linear. How could I do for analyzing were the unstability arises?

Thanks

 

[Baluncore]

You must understand the feedback mechanisms available in your model.
Reality and non-linear models will oscillate at pressure dependent flow rates.
You must restrict model parameter search variation to the domain that is free of oscillation.
You will therefore have to study the bounds of stability before further optimisation.

Unfortunately the best operating point is often right on the edge or regeneration.
There is a trade-off, maybe by optimisation you are designing an unreliable product.

 

[serbring]

Thanks Baluncore, is there any systematic way to search for that boundary or should I do by trials?

 

[Baluncore]

Trial and error is the simple learning approach. A programmed grid search in several parameters would work if you could quickly and reliably identify the onset of oscillation.
Don't forget you are only fine tuning the simplified model, not the real world device you believe you have modeled.

 

[Q_Goest]

Can you provide a cross sectional picture of the regulator you are trying to model? Can you describe your model so far? Things like the mass of the moving parts (poppet, stem, diaphragm backing plate, spring, etc...), flow restrictions through the valve (give consideration to how far open the valve actually is at anyone point in time), how upstream and downstream pressure reacts to the opening of the valve, etc... Can you provide a diagram of forces on the moving parts? What kind of time step you are using and is it is a variable in your program? What kind of output are you creating?

 

[serbring]

Hi all,

@Baluncore: thanks for your reply I'll try with a programmed grid.

@Q_Goest:

Can you provide a cross sectional picture of the regulator you are trying to model?

here a cross sectional picture of the regulatore I'm trying to model:

Can you describe your model so far? Things like the mass of the moving parts (poppet, stem, diaphragm backing plate, spring, etc...), flow restrictions through the valve (give consideration to how far open the valve actually is at anyone point in time), how upstream and downstream pressure reacts to the opening of the valve, etc...

Yes, I can describe the model and I'm developing a simscape model to reproduce the dynamic of the pressure regulator. Here a sketch with the forces of the moving parts:

Xop, xopp: free length of the poppet and piston spring
Xp, xpp: piston and poppet displacement
Fcp,pp: contact force between the poppet and the piston
Fcps,pp: contact force between the poppet and the poppet seat
kp, kp: stiffness of the piston and poppet spring
Fr: friction force
mp, mpp: mass of the piston and the popet

What kind of time step you are using and is it is a variable in your program?

I use a constant time step solver and the time step is 0.001s

What kind of output are you creating?

I'm trying to reproduce the pressure - flow rate curve of the pressure regulator I see in the datasheet and its step response. Here the pressure - flow rate curve I'm trying to fit:

[

I'm using an optimization solver to find the parameters that minimizes the SSE between the datasheet curves and the ones of the model. Moreover I have added non linear constraints to comply the valve step response specifications (i.e. rise and settling time and peak overshoot).

In order to get a similar dynamic behaviour of the pressure regulator with any set of paramaters, I have parametrized the spring stiffness in function of the valve max displacement (i.e. valve cross area) and the pressure differential between the outlet and the setpoint. In this way the valve is completely open with a specific pressure differential. This worked very well with a valve with the following kind of pressure - flow rate curve, because the max flow rate doesn't change with outlet pressure

[



But for the valve before mentioned graph the situation is different, higher pressure, higher flow rate, so I believe the area changes with pressure, but I didn't understand how to do it in my model. This is another open issue of my model. Maybe the spring parametrization is wrong?

Hopefully to have well stated my problems. Any suggestions is very appreciated.

cheers

 

[Baluncore]

The only mode of oscillation I can see in your poppet valve model is the delay in piston movement to counter the valve when it approaches closure. By changing the poppet valve for a spool valve the positive feedback chatter should be eliminated. Attached is an edit of your diagram.

 

[Q_Goest]

Hi serbring. Those graphs you posted show how a regulator responds to changes in flow rate given a fixed pressure setting on the regulator. For example, the regulator might be set at 1.2 bar at zero flow (ie: "lockup") and as the demand for flow increases, the pressure on the regulator outlet decreases as can be seen in the first graph.

The reason the outlet pressure on the regulator drops with an increase in flow isn't really a "dynamic" issue. The poppet in the regulator isn't changing position when that happens, it is in one position and it stays there while the system flows at the given flow rate. So when flow increases to 450 l/min, the pressure on the regulator has dropped to roughly 0.9 bar as shown on the graph. Note that I wouldn't trust the second graph you provided. It doesn't look like any actual data or any theoretical model of the regulator was taken into account on that one to be honest. A real graph of pressure versus flow for a regulator looks like the first graph you provided with a gradual drop off of pressure as flow increases. So I'll ignore the second graph for this discussion.

The diagram you provided is ok, though I didn't try to look at it in detail. I do see a few problems though. First, as mentioned before, the graph is looking at a valve without movement of the poppet or diaphragm. So there's no need to consider time rate dependent forces on the regulator. You also can neglect frictional forces if you'd like since those are generally small compared to the spring and pressure forces. If you're trying to model that graph you provide, you want to look at a static force diagram of the regulator with pressure causing a force on the poppet and diaphragm and spring forces causing forces where they exist.

Next, you will need to model the flow somehow. The valve poppet has some balance of forces when the valve is closed and pressure is at the set pressure of the regulator. At that point, the spring is providing a force exactly equal to the pressure forces when the poppet is closed. In reality, there's a problem with this simplistic model and that is that the seat needs to have a high enough contact force to seal the fluid, so the spring load is actually lower than the pressure forces at that point since you need some additional force to create the seal but for simplicity, I'll neglect that. We can come back to it later if you want.

The valve is closed at a given set pressure so we'll assume flow is zero at that point. That point on the graph shown above for example might be 1.2 bar with 0 flow (l/min). That's the point where forces are balanced and the poppet is touching the seat. Now the valve opens as pressure downstream where it is being sensed, drops. As pressure drops, the force on the diaphragm and poppet drop to a new, lower value. Since that force is lower, the spring will push the poppet open and come to equilibrium at a new location. When the spring extends like this, the force goes down according to the spring rate times the change in length of the spring, so the spring also has a lower force which must equal the lower pressure force. That's the point you need to determine for a given 'flow rate'. Actually what you need to determine is how far the poppet opens at that point and what the corresponding flow coefficient will be. It obviously won't be "full open" since that won't happen till the pressure decays enough to fully extend the spring and push the poppet to that point. So the full open point can be determined by determining the location of the poppet, the spring load at that point and the corresponding pressure load that puts the entire assembly into static equilibrium. That pressure will necessarily be lower than the set pressure which is why the curves on the graph drop as flow rate increases.

More on how to calculate the flow restriction of the poppet if you need it, just ask.

If you really want to understand how the regulator responds to a sudden change in pressure or an oscillating change in flow rate, then that would be a dynamic issue that requires calculating not just the instantaneous position and flow of the valve but also the inertia of the moving assembly and also the variation in pressure under the diaphragm if there is a restrictive orifice as you show in the diagram. That gets a bit more complicated, but I think you need to figure out how to model the valve flow restriction first and understand how that can create the graph you posted before moving on to a true dynamic model of a regulator.

 

[serbring]

The only mode of oscillation I can see in your poppet valve model is the delay in piston movement to counter the valve when it approaches closure. By changing the poppet valve for a spool valve the positive feedback chatter should be eliminated. Attached is an edit of your diagram.

I'll model the pressure force on the valve. Thanks!

Hi serbring. Those graphs you posted show how a regulator responds to changes in flow rate given a fixed pressure setting on the regulator. For example, the regulator might be set at 1.2 bar at zero flow (ie: "lockup") and as the demand for flow increases, the pressure on the regulator outlet decreases as can be seen in the first graph.

The reason the outlet pressure on the regulator drops with an increase in flow isn't really a "dynamic" issue. The poppet in the regulator isn't changing position when that happens, it is in one position and it stays there while the system flows at the given flow rate. So when flow increases to 450 l/min, the pressure on the regulator has dropped to roughly 0.9 bar as shown on the graph.

I got it, but if there will be 0.4bar of pressure differential between the outlet pressure and the setpoint, the spool displacement is 1mm (consequently a specific cross valve area) independently of the outlet pressure , right?

Note that I wouldn't trust the second graph you provided. It doesn't look like any actual data or any theoretical model of the regulator was taken into account on that one to be honest. A real graph of pressure versus flow for a regulator looks like the first graph you provided with a gradual drop off of pressure as flow increases. So I'll ignore the second graph for this discussion.

with my model I'm able to fit that chart, using the before mentioned spring parametrization: with 0.1bar of pressure differential between the outlet pressure and the setpoint the valve is completely open and it doesn't seem to happen to the valve of the following chart.

[GRAPH 1]

After a meditation, I'm wondering how would it be the GRAPH 1 if for each pressure level the regulator would be test to a 0 bar? Would it be something like that?

[GRAPH 2]

As far as I have understood in a chocked condition the valve flow rate is not dependent by the outlet pressure but only by the inlet pressure, the sonic conductance, the cross area and so on. So I would believe all the lines will drop to the same flow rate. In the GRAPH 1 all the lines don't look to drop at the same flow rate, right? So could it be possible that for the GRAPH 1 the inlet pressure at 6 bar test is different than the one at 10 bar test?

The diagram you provided is ok, though I didn't try to look at it in detail. I do see a few problems though. First, as mentioned before, the graph is looking at a valve without movement of the poppet or diaphragm. So there's no need to consider time rate dependent forces on the regulator. You also can neglect frictional forces if you'd like since those are generally small compared to the spring and pressure forces. If you're trying to model that graph you provide, you want to look at a static force diagram of the regulator with pressure causing a force on the poppet and diaphragm and spring forces causing forces where they exist.

The piston/diaphram dynamic is modeled, look at the rough sketch, xp is the piston displacement.

Next, you will need to model the flow somehow. The valve poppet has some balance of forces when the valve is closed and pressure is at the set pressure of the regulator. At that point, the spring is providing a force exactly equal to the pressure forces when the poppet is closed. In reality, there's a problem with this simplistic model and that is that the seat needs to have a high enough contact force to seal the fluid, so the spring load is actually lower than the pressure forces at that point since you need some additional force to create the seal but for simplicity, I'll neglect that. We can come back to it later if you want.

I modeled the flow using that simscape block:
http://www.mathworks.it/it/help/physmod/simscape/ref/variableareapneumaticorifice.html

But I didn't model the flow force to valve, but I'm going to do it.

The valve is closed at a given set pressure so we'll assume flow is zero at that point. That point on the graph shown above for example might be 1.2 bar with 0 flow (l/min). That's the point where forces are balanced and the poppet is touching the seat. Now the valve opens as pressure downstream where it is being sensed, drops. As pressure drops, the force on the diaphragm and poppet drop to a new, lower value. Since that force is lower, the spring will push the poppet open and come to equilibrium at a new location. When the spring extends like this, the force goes down according to the spring rate times the change in length of the spring, so the spring also has a lower force which must equal the lower pressure force. That's the point you need to determine for a given 'flow rate'. Actually what you need to determine is how far the poppet opens at that point and what the corresponding flow coefficient will be. It obviously won't be "full open" since that won't happen till the pressure decays enough to fully extend the spring and push the poppet to that point. So the full open point can be determined by determining the location of the poppet, the spring load at that point and the corresponding pressure load that puts the entire assembly into static equilibrium. That pressure will necessarily be lower than the set pressure which is why the curves on the graph drop as flow rate increases.

More on how to calculate the flow restriction of the poppet if you need it, just ask.

If you really want to understand how the regulator responds to a sudden change in pressure or an oscillating change in flow rate, then that would be a dynamic issue that requires calculating not just the instantaneous position and flow of the valve but also the inertia of the moving assembly and also the variation in pressure under the diaphragm if there is a restrictive orifice as you show in the diagram. That gets a bit more complicated, but I think you need to figure out how to model the valve flow restriction first and understand how that can create the graph you posted before moving on to a true dynamic model of a regulator.

I got it...I'll try first to model flow force to the poppet first.

Thanks to all, hopefully my doubts are clearly stated...if not, please ask me. :)

 

[serbring]

Hi all,

I'm trying to follow your suggestions: I modeled the flow force to the model in a easy way and the pressure fluctuation is lower than in the previous model.

Then I tried to identify the pressure regulator parameters to fit a reference pressure - flow rate cuve. I performed the identification with the an optimization solver and using the SSE as cost function.
The flow rate for all the curves are computed with an inlet pressure of 7 bar and using a ramp and a pressure source I change the outlet pressure during the simulation. The setpoint is constant during the simulation and it is set to the intial outlet pressure, so for the red curve, the setpoint is 6 bar and the outlet pressure changes linearly from 6 to 5 bar. Here you can see a sketch of my model:

Here the reference curve for the flow from 1 to 2:

Here the one of my model:

I can explain the curve of my model: I see the lookup, the drop and the choked flow condition. In my model the flow rate in the choked condition doesn't change with the outlet pressure, instead for the reference curves it looks to change and I can't understand the reason of it. Is the valve Cd (Discharge coefficient) pressure dependent? Does the valve open more at higher pressure than in lower ones? In this case why? Could it be the case the reference curve are created with different inlet pressure? Any suggestion is appreciated

Thanks

CheersSerbring

 

[Q_Goest]

Hi serbring. I can't tell for sure what you're doing in your model, but the output graphs look reasonable. First, let's talk about "flow force". I'm not sure what you mean by that but I assume you're referring to the force exerted on the poppet due to the change in momentum of the gas as it impinges on the poppet as opposed to the force produced by the difference in pressure across the poppet. The former is small and can generally be neglected. The latter is significant for an unbalanced regulator such as the type you show in the picture. A balanced regulator has a poppet that has the same pressure on both ends so that the forces on the poppet during operation are the same and can be neglected.

You should have a calculation that shows shows how the forces are balanced in a static condition. That force balance calculation determines the poppet lift. The poppet lift gives you curtain area which is the cylindrical area around the opening of the poppet. That curtain area is the circumference times the height. That area is your flow restriction which, when multiplied by your discharge coefficient, gives you the valve's flow capacity. The flow is then calculated per that link you provided here:
http://www.mathworks.com/help/physmod/simscape/ref/variableareapneumaticorifice.html

Note that the link you provided also gives the equation for the critical pressure ratio which tells you if the flow across your poppet is choked or not. If flow is choked AND if the valve poppet has come full open, the line on those graphs goes vertical which you can see on some of the graphs above. On those graphs that don't show a vertical section of line, the valve poppet hasn't gotten to the 'full open' position yet, so a drop in the downstream pressure allows the poppet to open more, increasing C_dA and increasing flow. It's only once your poppet has reached it's maximum lift (max open) that you no longer get any increase in flow by decreasing downstream pressure. That statement assumes of course, that flow is choked at the poppet curtain area.

Regarding discharge coefficient, the discharge coefficient can certainly change as the valve poppet changes position and even as the pressures change. The discharge coefficient in this case is like a 'catch all' for various things that can affect the flow. Note that normally discharge coefficient for an orifice has a more specific meaning regarding the vena contracta. It means the same here but the flow geometry is obviously a bit more complex.

 

[serbring]

Hi Q_Goest,

thanks for your helpful reply, it took a while to meditate about it. Firstly I didn't understand that the poppet could be not fully open with lower outlet pressure. I was firstly mislead by the first valve graph with the straight lines and actually I still don't understand how it happens.

Regarding the flow force I meant the force produced by the poppet pressure unbalance. I changed the poppet with a balanced one as suggest by Baluncore. In my model the poppet dynamic is affected only by the spring stiffness and the pressure differential between the outlet pressure and the setpoint. So I have modeled somehow that poppet pressure unbalance. Here a sketch of the model:

From the force equilibrium equation I derived the valve area relationship with the outlet pressure P$_{out}$ during the charging. In calculating it I supposed that there is a sharp boundary where the pressure act. So:
$A_{s0}$: area where the inlet pressure acts when the poppet is fully closed
$A_{o0}$: area where the inlet pressure acts when the poppet is fully closed
$A_p$: poppet opening area
$A_d$: area of the lower side of the poppet
$A_s=A_{s0}+A_p cos(\theta)$: relation between the area where the inlet pressure acts and the poppet opening area
$A_o=A_{o0}-A_p cos(\theta)$: relation between the area where the outlet pressure acts and the poppet opening area
$\theta$: poppet conical angle
$A$: piston area
$x_{p}, x_{pp}$: piston and poppet displacement
$x_{op}, x_{opp}$: piston and poppet spring free lengthHere the force equilibrium:

[1] $k_p (x_{op}-x_p)- P_{out}A- k_{pp}(x_{opp}-x_{pp})+P_{out}(A_s cos(\theta) -A_d)+P_{in}*A_s cos(\theta)=0$

I rearranged the equation [1] for deriving $A_p$in function of $P_{out}$ for: $P_{set}=k_p*x_op$, $\Delta P=P_{set}-P_{out}$, $k_{pp}=k_p$ and $x_p=x_{pp}$:

[2] A$_{P}=\frac{P_{in}(A_{s0}cos(\theta)-A_{d})-K_{pp}x_{0pp}+\Delta P A+P_{out}A_{o0}*cos(\theta)}{{cos(\theta)}^{2}(P_{in}+P_{out})}$

Here the derivative of the equation [2] with respect the outlet pressure (Pout):

[3] $\frac{d A_{P}}{d P_{out}}=\frac{k_{pp}x_{0pp}+P_{in}(A_d+cos( \theta )(A_{o0}-A_{s0}))-\Delta P A}{{cos(\theta)}^{2}(P_{in}+P_{out})}$

it seems the valve area decrease with increasing of Pout, so it should be more open with lower outlet pressure and that it's not like that from the valve flow rate - pressure curve (here the curve again):

I tried to change the balanced poppet with unbalanced one, but it doesn't change the story.

Here a technical drawing of the valve I'm trying to model:

I still don't the why the pressure regulator behaves like that. Is there an effect I didn't take into account?

Thanks

cheers

 

[Q_Goest]

Hi serbring. I went through your post and I’m a bit confused. Equation 1 looks fine. I see you’re using forces downward as being positive and forces up as being negative. I’m not sure if you’re using angles properly, I wouldn’t worry too much about it though. I assume you’ve just rearranged equation 1 to get equation 2 so that’s fine. But I’m not sure about equation 3. Why do you want to take a derivative like that? I see no need to do that and I’m not sure what that even physically represents.

Let’s look at a simplified model for a second, then you can go back to adjusting it for valve poppet angles and so on. For a balanced poppet, we can neglect pressure forces on the poppet and let’s also neglect the second spring you show that’s under the poppet. You can add those in later. That leaves you with force down from the spring is equal to force up due to pressure on the diaphragm. Now let’s consider a simple example using the following values for our regulator:
Diaphragm area = 10 square inches
Spring rate = 1000 pounds per inch
Set pressure = 100 psig

For this regulator, the force up due to pressure is just the diaphragm area times the pressure: 10 square inches * 100 psi = 1000 pounds.
To have the regulator ‘set’ at this point, we need the valve to just come closed at 100 psi, so the spring is almost able to push the poppet off the seat but not quite. So the spring has to push down with a force of 1000 pounds which means that it has to be compressed by x = F/k. So the spring is being compressed 1 inch.

If we took all the pressure off of the regulator and if the spring could actually move the poppet at that point, the poppet would open 1 inch. However, if pressure dropped to only 90 psig, you have a force upwards of 90 psi times the diaphragm area of 10 square inches or 900 pounds. Looking at the spring again, the spring is only compressed 0.9 inches. So with a discharge pressure of 90 psig this particular regulator has a poppet that’s open exactly 0.1 inches.

Once you know how far the poppet is open, you can calculate flow. Let’s say our poppet diameter is 1” and at a set pressure of 100 psi, it has a 0.1” opening when outlet pressure drops to 90 psi. The flow restriction through this valve is given by the curtain area which is the circumference times the height. So that’s 1” * .1” * pie = 0.314 square inches. That opening may have a discharge coefficient of 0.7, but that will be a function of the valve’s geometry and is generally only derived experimentally. From my experience, it generally is in the range of 0.6 to 0.8. Now if you have some inlet pressure you can calculate the flow rate by going to that web page you pointed to before. You have upstream pressure, downstream pressure and your C_dA (discharge coefficient times area which is your flow restriction).

The graph you posted has numerous lines. Each line is a set point for that regulator. The lowest line shows a set point of 1.2 bar. Wherever you got this graph from, it should tell you what it assumes for an upstream pressure. The graph doesn’t say, but that is implied somewhere, wherever you got the graph. If you did an analysis on the regulator that you got the graph from, you should be able to sum the forces as shown above, determine how far open the valve poppet is at any given discharge pressure, determine the corresponding flow restriction, and from the pressures on the inlet and outlet of your regulator, you should be able to calculate the flow and come up with the graph.

Note that as long as your regulator poppet continues to open (and presumably the flow restriction goes down, which is a function of geometry) the flow rate should go up, regardless of whether or not it is choked. Because as the poppet opens, you get a larger flow area (curtain area). Once the poppet is fully opened and the flow restriction stops changing with downstream pressure, and assuming the valve is choked, lowering the downstream pressure isn’t going to change anything.

Hope that helps.

 

[serbring]

Hi Q_Goest,


Thanks for your helpful reply, maybe there was a misunderstanding about my doubt, I will be clearer. I 'm sorry for it.
Thanks to you, I found a mistake on the angles of the equation 1 ( :) ): I have to change the $cos(\theta)$ with $sin(\theta)$. Unfortunately I can't edit anymore the formula of the previous post. I derived the equation 3, because as far as I uderstood the poppet displacement isn't only dependent by the pressure differential between the outlet pressure and the setpoint. Look at the following graph:

at the point A the outlet pressure is dropped of 0.2 bar as at the point B, but at the point A the poppet displacement is higher than for the point B, otherwise the flow rate should be the same, right?

Supposing a simple pressure regulator, I can calculate the force balance equation:

[1] $k_p (x_{op}-x_p)- P_{o} A=0$

But $k_p*x_{op}=P_{set}A$

Therefore:

[2] $-k_{p} x_p + (P_{set}-P_{o})A=0$

So the equation of the poppet displacement is $x_p$:

[3] $x_è=\frac {(P_{set}-P_{o})A }{k_p}$

The equation 3 can't explain why the poppet displacement is higher for the point A than for the point B. So I thought the poppet force unbalance might explain it. For this reason I calculated the derivative of the previous post and I believe it can explain how the poppet area will change with the increasing of $P_{o}$ in a static condtion. Anyway my statement about the derivative was wrong: it isn't always positive with $P_{o}$ but it depends by the other equation parameters.

My big doubts are: why the poppet displacement at the point A is higher than at the point B? Why the the flow rate for point C is higher than point D?


Thanks again. :)

Cheers

 

[Q_Goest]

Hi serbring,
I’m trying to determine what your notation is. You posted some earlier:
$A_{s0}$: area where the inlet pressure acts when the poppet is fully closed
$A_{o0}$: area where the inlet pressure acts when the poppet is fully closed
$A_p$: poppet opening area
$A_d$: area of the lower side of the poppet
$A_s=A_{s0}+A_p cos(\theta)$: relation between the area where the inlet pressure acts and the poppet opening area
$A_o=A_{o0}-A_p cos(\theta)$: relation between the area where the outlet pressure acts and the poppet opening area
$\theta$: poppet conical angle
$A$: piston area
$x_{p}, x_{pp}$: piston and poppet displacement
$x_{op}, x_{opp}$: piston and poppet spring free length

Then you have what seems like a problem equation:
[1] $k_p (x_{op}-x_p)- P_{o} A=0$
Which is your force balance for a simple regulator. It says the spring rate times the quantity: free length of the spring minus the piston displacement, minus the pressure Po times the ‘piston area’ (assume that is your diaphragm effective area for a diaphragm type regulator or the piston area for a piston style regulator) and that all equals zero for static balance. You don’t say what Po is but I assume that is your actual outlet pressure which I assume is supposed to be equal to or less than the set pressure.

But look at the spring force in that equation... Spring force is supposed to be spring rate times how much the spring is compressed. That’s not what you have in the equation. For that spring displacement part of your equation, you need to show how much this spring is compressed. So the amount of compression in your spring (dx) is the free length minus the compressed length, right? The length of the spring after you’ve compressed it has to be subtracted from the free length to give you how much the spring has been compressed which is dx. Then multiply by spring constant to get your force.

Then you say:

$k_p*x_{op}=P_{set}A$

Which is spring rate of the piston spring times the free length of the spring which has to equal the set pressure times the area. But spring rate times free length gives you a force equal to the force of compressing the spring so that it is absolutely flat and has no height at all.

Now let’s go back to one of your questions. You asked:

… as far as I understood the poppet displacement isn't only dependent by the pressure differential between the outlet pressure and the set point.

Let’s talk about a pressure balanced regulator first since that’s a bit easier to understand and you can always modify your equations later to add in additional forces due to pressure and spring loads on the poppet. Equation 1 above should reduce to something like k dx = PA where dx is how much the spring has been compressed (free length minus compressed length). So for some change in pressure (dP) the only thing we have in that equation to make it balance is dx, so dP is linearly proportional to dx. Do you agree? If so, then for any absolute change in pressure, dP, the regulator poppet has to react by changing displacement, dx and those terms are linearly related. Poppet displacement therefore is only dependent on the pressure differential between the outlet pressure and the set point. For the graph in question, point A and point B both show a difference in pressure differential between the outlet pressure and the set point of 0.2 bar, so the valve poppet has opened the same amount in both cases.

NOTE: The graph doesn’t tell you if the springs used in the regulator are the same or not and it doesn’t tell you what the upstream pressure is. Generally, regulator manufacturers will have numerous different springs for their regulators to handle different outlet pressure ranges because they try to optimize the valve for the pressure range the valve will be operating in. So we can’t say for sure that the amount of poppet opening for those two cases are necessarily the same, but if the same spring was used for each case, then the poppet opening is also the same.

 

[serbring]

Hi serbring,
I’m trying to determine what your notation is. You posted some earlier:
$A_{s0}$: area where the inlet pressure acts when the poppet is fully closed
$A_{o0}$: area where the outlet pressure acts when the poppet is fully closed
$A_p$: poppet opening area
$A_d$: area of the lower side of the poppet
$A_s=A_{s0}+A_p cos(\theta)$: relation between the area where the inlet pressure acts and the poppet opening area
$A_o=A_{o0}-A_p cos(\theta)$: relation between the area where the outlet pressure acts and the poppet opening area
$\theta$: poppet conical angle
$A$: piston area
$x_{p}, x_{pp}$: piston and poppet displacement
$x_{op}, x_{opp}$: piston and poppet spring free length

Hi Q_Goest,

Thanks for your helpful reply.
I'm sorry, I changed the subscript for the outlet pressure, let's use $P_o$ for it. There was a mistake in the symbol list, I corrected it as you can see in the bolded text in quote. Here a valve sketch that hopefully will help you to understand my notation:

The dotted lines represent the poppet when it's open.

Then you have what seems like a problem equation:
[1] $k_p (x_{op}-x_p)- P_{o} A=0$
Which is your force balance for a simple regulator. It says the spring rate times the quantity: free length of the spring minus the piston displacement, minus the pressure Po times the ‘piston area’ (assume that is your diaphragm effective area for a diaphragm type regulator or the piston area for a piston style regulator) and that all equals zero for static balance. You don’t say what Po is but I assume that is your actual outlet pressure which I assume is supposed to be equal to or less than the set pressure.

But look at the spring force in that equation... Spring force is supposed to be spring rate times how much the spring is compressed. That’s not what you have in the equation. For that spring displacement part of your equation, you need to show how much this spring is compressed. So the amount of compression in your spring (dx) is the free length minus the compressed length, right? The length of the spring after you’ve compressed it has to be subtracted from the free length to give you how much the spring has been compressed which is dx. Then multiply by spring constant to get your force.

Then you say:

$k_p*x_{op}=P_{set}A$

Which is spring rate of the piston spring times the free length of the spring which has to equal the set pressure times the area. But spring rate times free length gives you a force equal to the force of compressing the spring so that it is absolutely flat and has no height at all.

I say:

$k_p*x_{op}=P_{set}A$

Because when: $P_{set}=P_o$, the valve must be closed, so $x_p=0$. Under this assumption my model regulates properly the outlet pressure.

Now let’s go back to one of your questions. You asked:

Let’s talk about a pressure balanced regulator first since that’s a bit easier to understand and you can always modify your equations later to add in additional forces due to pressure and spring loads on the poppet. Equation 1 above should reduce to something like k dx = PA where dx is how much the spring has been compressed (free length minus compressed length). So for some change in pressure (dP) the only thing we have in that equation to make it balance is dx, so dP is linearly proportional to dx. Do you agree? If so, then for any absolute change in pressure, dP, the regulator poppet has to react by changing displacement, dx and those terms are linearly related.

I completely agree with it.

Poppet displacement therefore is only dependent on the pressure differential between the outlet pressure and the set point. For the graph in question, point A and point B both show a difference in pressure differential between the outlet pressure and the set point of 0.2 bar, so the valve poppet has opened the same amount in both cases.

Why the valve flow rate is higher for point A then point B? I can't explain it.

NOTE: The graph doesn’t tell you if the springs used in the regulator are the same or not and it doesn’t tell you what the upstream pressure is. Generally, regulator manufacturers will have numerous different springs for their regulators to handle different outlet pressure ranges because they try to optimize the valve for the pressure range the valve will be operating in. So we can’t say for sure that the amount of poppet opening for those two cases are necessarily the same, but if the same spring was used for each case, then the poppet opening is also the same.

The curves are for a specific valve range (0-2 bar) so I would believe that is the spring rate is the same for all curves. Regarding the downstream pressure, I have few dobts about it, but I talked with the sales man and he said (in not confidently way) that it is the same. In fact in another page of the catalogue I have found the flow rate - pressure chart for the same valve but with a different nominal diameter there is this :

The choked condition is the same so I would believe the upstream pressure is the same for all curves.


Thanks again for your preciuos help! :)

Cheers

 

[Q_Goest]

Hi serpring,

I say:

$k_p*x_{op}=P_{set}A$

Because when: $P_{set}=P_o$, the valve must be closed, so $x_p=0$. Under this assumption my model regulates properly the outlet pressure.

So are you saying that $x_{op}$ is equal to the amount the spring is compressed? For example, if a spring has a free length of 2 inches and it’s compressed half an inch then it’s 1.5 inches long at P_set but $x_{op}$ is equal to half an inch. Would you agree?

Why the valve flow rate is higher for point A then point B? I can't explain it.

I just noticed that the graph you are referring to is for an electronic regulator built by http://ftp.festo.com/public/PNEUMATIC/SOFTWARE_SERVICE/PDF_Catalogue/PDF/US/VPPM-G_ENUS.PDF. It is not a conventional, spring loaded regulator such as the ones we’ve been talking about. There are various ways to produce the force needed to open the valve. One way is to use a spring. Another very common way is to use the pressurized gas upstream of the regulator. There are various ways of using this gas. One way is to “dome load” a regulator using a conventional spring loaded regulator. Using this method, you have a simple, spring loaded regulator (preferably a 'self relieving' type) that puts gas pressure above the diaphragm or piston. That pressure pushes down just like a spring but because the volume of gas is generally fairly large compared to the displacement, a regulator loaded this way can more accurately control the outlet pressure. Basically, the equivalent spring rate of the gas is low compared to a spring.

Another way is to have some electronic valves that adjust the pressure in the dome of the regulator. This should also help to control outlet pressure but the primary reason to do this is to allow for electronic control. So with this type of arrangement, the controls and electric circuits will have some influence on the regulator outlet pressure. It isn't a simple spring arrangement. That's what the Festo regulator is doing. So our discussion around the spring loading of the regulator isn't applicable. This regulator isn't a spring loaded one.

 

[serbring]

Hi serpring,


So are you saying that $x_{op}$ is equal to the amount the spring is compressed? For example, if a spring has a free length of 2 inches and it’s compressed half an inch then it’s 1.5 inches long at P_set but $x_{op}$ is equal to half an inch. Would you agree?

Hi Q_Goest,

Thanks again for your helpful reply. I assume $x_{op}= 2$, because the spring is compressed when $P_o > P_{set}$ and it is extended when $P_o < P_{set}$. It's not probably true because this means to change the spring anytime the setpoint is changed. I was looking for a quick way to model it. Is there any better way of modeling it?

I just noticed that the graph you are referring to is for an electronic regulator built by http://ftp.festo.com/public/PNEUMATIC/SOFTWARE_SERVICE/PDF_Catalogue/PDF/US/VPPM-G_ENUS.PDF. It is not a conventional, spring loaded regulator such as the ones we’ve been talking about. There are various ways to produce the force needed to open the valve. One way is to use a spring. Another very common way is to use the pressurized gas upstream of the regulator. There are various ways of using this gas. One way is to “dome load” a regulator using a conventional spring loaded regulator. Using this method, you have a simple, spring loaded regulator (preferably a 'self relieving' type) that puts gas pressure above the diaphragm or piston. That pressure pushes down just like a spring but because the volume of gas is generally fairly large compared to the displacement, a regulator loaded this way can more accurately control the outlet pressure. Basically, the equivalent spring rate of the gas is low compared to a spring.

Another way is to have some electronic valves that adjust the pressure in the dome of the regulator. This should also help to control outlet pressure but the primary reason to do this is to allow for electronic control. So with this type of arrangement, the controls and electric circuits will have some influence on the regulator outlet pressure. It isn't a simple spring arrangement. That's what the Festo regulator is doing. So our discussion around the spring loading of the regulator isn't applicable. This regulator isn't a spring loaded one.

You're on right. I haven't understood that much the technical drawing you can see in one of my previous posts, but as far as I have understood the diaphrams is pushed down by a solenoid, right? So somehow the pushing force is related to a voltage, right?
So under this light the valve areas for the points A and B are still the same? Moreover I don't understand why the max flow rate for the line starting from 2bar (point C) is higher than the line starting from 1.2 bar (point D).
Do you have any suggestion about modeling that kind of valve? Actually I'm completely confused, after 3 months of modeling that valve I still don't have a good model of a pressure regulator and I don't have any how moving forward.

Cheers

 

[Q_Goest]

Hi serbring,

I assume $x_{op}= 2$, because the spring is compressed when $P_o > P_{set}$ and it is extended when $P_o < P_{set}$. It's not probably true because this means to change the spring anytime the setpoint is changed. I was looking for a quick way to model it. Is there any better way of modeling it?

It sounds like you are having some trouble with modeling the spring force. The force exerted by a spring is equal to the spring constant times the amount of compression. F = k dx. So for a spring load of 100 lb/in for example, for every inch the spring is compressed, the force increases by 100 lb. So compress 1 inch, the force is 100 lb. Compress 2 inches, the force is 200 lb. Etcetera.

This particular regulator uses a diaphragm for its sensing element so if the area is 10 square inches and has a pressure on it equal to 1 bar, then the force is 145 lb. In that case, the spring has to produce a force of 145 lb, so it has to be compressed 1.45 inches. Note that 100 lb/in * 1.45 inches = 145 lb. That equals the force on the diaphragm so that they are in equilibrium.

… as far as I have understood the diaphrams is pushed down by a solenoid, right? So somehow the pushing force is related to a voltage, right?

I’m sorry but that’s incorrect. The diaphragm is pushed down by the air which is regulated into the chamber (sometimes called a “dome”) above the diaphragm. I would guess that there are solenoid valves to control the air pressure in the dome. The voltage isn’t directly related to the pressure.

So under this light the valve areas for the points A and B are still the same?

That’s not something you can tell from this analysis because it isn’t a spring loaded regulator. The gas pressure can be highly nonlinear and follow a different curve for each setting.

Regarding modeling this valve, why do you need to model it? Is this a school project? If you want to model it, you need a lot of details about the valve such as dimensions, spring constants, volumes, how the electronics are used to control the set pressure, etc... You also need to figure out how it works. Perhaps you can explain why you're modeling this and how accurately you need to do so.

 

[AlephZero]

Instead of trying to model the physics (difficult) and electronic control system (impossible unless you know how it is designed), you could attack this from the other direction. You said you have a plot of the step response of the device, as well as the steady-state response curves you have shown. So do a "system identification" exercise to find the transfer function from the step response.

I don't know what theoretical background you have, but the details should be covered in courses on control systems theory, or experimental vibration measurement.

 

[serbring]

Hi serbring,

It sounds like you are having some trouble with modeling the spring force. The force exerted by a spring is equal to the spring constant times the amount of compression. F = k dx. So for a spring load of 100 lb/in for example, for every inch the spring is compressed, the force increases by 100 lb. So compress 1 inch, the force is 100 lb. Compress 2 inches, the force is 200 lb. Etcetera.

Hi Q_Goest,

You're on right, infact for me the spring force is $k_p (x_{op}- x_p )$ but in my model the $x_{op}$ is calibrated with the setpoint. Isn't it fine?

This particular regulator uses a diaphragm for its sensing element so if the area is 10 square inches and has a pressure on it equal to 1 bar, then the force is 145 lb. In that case, the spring has to produce a force of 145 lb, so it has to be compressed 1.45 inches. Note that 100 lb/in * 1.45 inches = 145 lb. That equals the force on the diaphragm so that they are in equilibrium. I’m sorry but that’s incorrect. The diaphragm is pushed down by the air which is regulated into the chamber (sometimes called a “dome”) above the diaphragm. I would guess that there are solenoid valves to control the air pressure in the dome. The voltage isn’t directly related to the pressure.

I believe the solenoid push down the diaphram because on the diaphram there are two metal blocks and I can't see in the technical drawing the air inlet to the "dome!" . Here you can see what the two metal blocks I mean:

I'm sorry for not using the precise words. Anyway since it is pushed down by air it is easier for me to model it. On the catalogue there is a relation between the control voltage and the setpoit. Is the voltage directly related to a force?

That’s not something you can tell from this analysis because it isn’t a spring loaded regulator. The gas pressure can be highly nonlinear and follow a different curve for each setting.

Regarding modeling this valve, why do you need to model it? Is this a school project? If you want to model it, you need a lot of details about the valve such as dimensions, spring constants, volumes, how the electronics are used to control the set pressure, etc... You also need to figure out how it works. Perhaps you can explain why you're modeling this and how accurately you need to do so.

It's not a school project, I'm designing the pneumatic actuation of a big friction brake that must be controlled by a pressure regulator and then through a PID controller I control the braking torque. So the model will allow me to check the design and to tune the PID controller. I have contacted Festo for helping me in selecting the pressure regulator and they suggested me that one. I don't need an accurate model of the valve and therefore in the first instance I tried with a spring loaded regulator and probably it would work fine if the max flow rate would have been the same for line in the chart. I'm thinking to change the valve max area in function of the inlet pressure with a lockup table. What do you think?

Instead of trying to model the physics (difficult) and electronic control system (impossible unless you know how it is designed), you could attack this from the other direction. You said you have a plot of the step response of the device, as well as the steady-state response curves you have shown. So do a "system identification" exercise to find the transfer function from the step response.

I don't know what theoretical background you have, but the details should be covered in courses on control systems theory, or experimental vibration measurement.

Hi AlephZero,

This is interesting. I don't know that much about system identification and for this reason I tried with physical modeling and an optimization technique as parameter identification method that are the tools I know. Since I need to model just the valve dynamics it is fine too and I don't want to model some details more without getting any further improvements that it is what I have been doing for the last 3 months. Should I use a similar approach like this one , right? But also using this method I have to know the valve physical dynamics, right?

Thanks to all

Cheers

 

[AlephZero]

What to do depends very much on what data you have. If life is simple and the step response is more or less independent of any other parameters, you could use it directly to model the time-domain behavior. Read a table of numbers from the step response graph, convert them into the impulse response, and you have the response to each time-step's worth of excitation.

Similarly you can easily convert the numerical step function response into a transfer function (by doing an Fourier transform), and use that as a numerical model in the frequency domain.

You don't necessarily have to fit a theoretical model to the data at all. Using measured transfer functions etc in numerical models is fairly standard in some application areas.

I don't have any expertise on modeling this sort of regulator, though, and I'm not a fluid dynamics guru.

 

[Q_Goest]

Hi serbring,

I believe the solenoid push down the diaphram because on the diaphram there are two metal blocks and I can't see in the technical drawing the air inlet to the "dome!" . Here you can see what the two metal blocks I mean:

I guess this is just a side note at this point, but the metal block you point to is a backing plate for the diaphragm. It supports the diaphragm, it's not being pushed on by a solenoid.

Anyway since it is pushed down by air it is easier for me to model it. On the catalogue there is a relation between the control voltage and the setpoit. Is the voltage directly related to a force?

These kinds of regulators need a signal to tell the regulator what the pressure set point needs to be. There are two fairly common methods I've seen, current and voltage. So what Festo is telling you is that you need to provide the regulator a voltage which corresponds to a pressure set point. That voltage signal doesn't need to change unless you want the set point to change, so you would just keep it at some fixed value. I'm not very familiar with how process controls produce that voltage and all the other necessary control issues (you have to also provide power to the reg) but that's basically what's going on. So for example, if they're asking for a 0 - 5 volt signal to set the regulator, that will correspond to a set pressure, for example 0 to 5 barg. If you send it 0 volts, the set pressure goes to 0 psig. Send it 1 volt, set pressure is 1 barg. Send it 5 volts, it goes to 5 barg, etc... You need to find out what the ranges are, but at that point the regulator has a set point that it tries to control to.

It's not a school project, I'm designing the pneumatic actuation of a big friction brake that must be controlled by a pressure regulator and then through a PID controller I control the braking torque. So the model will allow me to check the design and to tune the PID controller. I have contacted Festo for helping me in selecting the pressure regulator and they suggested me that one. I don't need an accurate model of the valve and therefore in the first instance I tried with a spring loaded regulator and probably it would work fine if the max flow rate would have been the same for line in the chart. I'm thinking to change the valve max area in function of the inlet pressure with a lockup table. What do you think?

Do you need to control the regulator set point using electronics? If you don't, perhaps you can get a conventional, spring loaded regulator. If you need electronic control and this is going to be the reg you want, then what is it that you really need to model? Do you need flow rate versus discharge pressure? Can you simply create an equation or create a look up table to model this? If you need flow as a function of outlet pressure, you can use the outlet pressure on your x axis, and calculate for flow (y axis) and simply curve fit a line such as shown on the attached.

 

[serbring]

What to do depends very much on what data you have. If life is simple and the step response is more or less independent of any other parameters, you could use it directly to model the time-domain behavior. Read a table of numbers from the step response graph, convert them into the impulse response, and you have the response to each time-step's worth of excitation.

Similarly you can easily convert the numerical step function response into a transfer function (by doing an Fourier transform), and use that as a numerical model in the frequency domain.

You don't necessarily have to fit a theoretical model to the data at all. Using measured transfer functions etc in numerical models is fairly standard in some application areas.

I don't have any expertise on modeling this sort of regulator, though, and I'm not a fluid dynamics guru.

Hi AlephZero,

thanks for your reply. The model is non linear so the step response changes with other parameters, such as the outlet volume. I used a bit the MATLAB system identification toolbox but just for doing some didactic experiments (only LTI systems) when I was a student. I will try to check it for non linear ones, could it be fine?

Cheers

 

[serbring]

Hi serbring,

I guess this is just a side note at this point, but the metal block you point to is a backing plate for the diaphragm. It supports the diaphragm, it's not being pushed on by a solenoid.


These kinds of regulators need a signal to tell the regulator what the pressure set point needs to be. There are two fairly common methods I've seen, current and voltage. So what Festo is telling you is that you need to provide the regulator a voltage which corresponds to a pressure set point. That voltage signal doesn't need to change unless you want the set point to change, so you would just keep it at some fixed value. I'm not very familiar with how process controls produce that voltage and all the other necessary control issues (you have to also provide power to the reg) but that's basically what's going on. So for example, if they're asking for a 0 - 5 volt signal to set the regulator, that will correspond to a set pressure, for example 0 to 5 barg. If you send it 0 volts, the set pressure goes to 0 psig. Send it 1 volt, set pressure is 1 barg. Send it 5 volts, it goes to 5 barg, etc... You need to find out what the ranges are, but at that point the regulator has a set point that it tries to control to.

Do you need to control the regulator set point using electronics? If you don't, perhaps you can get a conventional, spring loaded regulator. If you need electronic control and this is going to be the reg you want, then what is it that you really need to model? Do you need flow rate versus discharge pressure? Can you simply create an equation or create a look up table to model this? If you need flow as a function of outlet pressure, you can use the outlet pressure on your x axis, and calculate for flow (y axis) and simply curve fit a line such as shown on the attached.

Hi Q_Goest,

thanks for your helpful reply. Yes, I need to control constantly the regulator set point constantly using electronics: an hardware read the braking torque through a sensor and from the error with the reference torque (it changes constantly) and it computes the correction to get the desired torque. As I said I need a dynamic model to tune a PID controller to control the valve. It's a standard Hardware in the loop simulation. For me even a neural network should work fine, as I said I just need to reproduce quite well the valve dynamic, so it's much more important to fit the step response than the steady one, but both of them are related each other. I want to model the flow rate versus the discharge pressure through a lockup table, but I have to understand how to introduce it in my model. Changing the area gradient in function of the pressure?

Thanks

Cheers

 

[Q_Goest]

Hi serbring, Thanks for your very courteous responces. I think AlephZero, yourself and I are in agreement that a model of the regulator based on basic principals isn't going to be a solution for you. Perhaps we could consider a higher level model of this system. Can you provide a process flow diagram (ie: a simplified P&ID - Process and Instrumentation Diagram) showing the key components including this regulator, the brake assembly, the torque measurement, what this brake assembly is driving and any other key components such as vent valves, accumulators/tanks or other components? Please also include the source gas (ie: air? pressure?). I'd like to understand also what happens to the air once it gets regulated and is used by this brake, does it get vented somewhere? I understand that you may not be able to share this information, but it might help to understand what you're trying to accomplish.

Cheers.

 

[serbring]

Hi Q_Goest,

Thanks for your helpful reply. Unfortunately I would prefer to not share publicly the plant layout. By the way it is quite simple: there is just a compressore, a dryer, a tank, a regulator and a spring acting return cylinder that moves the brake pad against the disc. The tank is necessary to have a stable regulator inlet pressure. The spring acting return cylinder have a a dead volume of 1l but it changes during the usage due to the braking pad wear, but I will consider it later. The source gas is air.
The torque is measured with strain gauge attached to the brake shaft. The outlet 3 of the regulator is vented directly to the atmoshere.
Hopefully that it is enough, otherwise, just ask.

Just another doubt regarding the valve curves. I was just reading the specification of the valve Festo vppe, that it has a much simpler layout because it doesn't have any electronic control. The flow rate - pressure curves are quite similar to the ones of VPPM, here the curve:

The flow rate is not linear with the pressure differential (the read line links al the point with the same pressure differential between the outlet pressure and the setpoint for each curve), so I'm wondering: can it be due to the pilot?

Thanks

cheers

 

[Q_Goest]

Hi serbring,

The flow rate is not linear with the pressure differential (the read line links al the point with the same pressure differential between the outlet pressure and the setpoint for each curve), so I'm wondering: can it be due to the pilot?

The regulator's flow rate is a function not only of how far open the poppet is, but also of the upstream and downstream pressures. We can't telll from the graphs, and Festo doesn't tell you, what the upstream pressure is for each of those curves. If the upstream pressure is the same for every curve, I would expect the lower set pressure curves to be out farther to the right than the higher set pressure curves. But that's not the case. It's just the opposite. However, if the upstream pressure is always some small dP above the outlet set pressure, say 1 bar for example, we would expect the curves to look as they do with the higher set pressure curves further out to the right. If you want to understand why that is true, do a calculation on flow through a valve at a fixed C_v and a fixed dP and vary the inlet pressure. You should find that as you increase inlet pressure, flow rate gradually increases. This will give you the red line in your graph that gradually drifts to the right as you increase pressure.

On page 17 of the Festo manual, they have a note next to inlet pressure that says the inlet pressure should always be 1 bar greater than the maximum regulated outlet pressure. I suspect that's where they get the graphs from, the inlet pressure for each of those set pressure lines is for a regulator with an inlet pressure 1 bar above the set pressure. But I can't tell you for sure that's how they came up with those graphs. I realize you want to use these graphs to create your control software and to size things in your system but if you are that concerned about the accuracy of those curves, then at the very least, I'd contact Festo and ask them how they came up with those curves and what the upstream pressure for each line is. If it's 1 bar above the outlet pressure, that won't help you much since your inlet pressure is likely to be significantly higher than 1 bar above set.

Regarding the P&ID you sent, I see also that you are assuming this is a self relieving regulator. Looking at the cross section and reading the literature, I believe you're correct. A self relieving regulator actually has 2 valves inside for controlling pressure. It has one that pressurizes the downstream port and one that vents the downstream port when pressure goes too high. In this case, it looks like the Festo regulator vents directly to atmosphere which is a common way to do it. The only other way is to provide a port that a tube or pipe can be connected to in order to vent the gas away. That's commonly done for hazardous gasses such as flammables or toxic gasses.

What you should know is that there's a hysteresis between the pressurization set point (and the one valve opening), and the vent set point (which allows the second valve to open). If you're below the pressurization set point and above the vent set point, both valves are closed and the downstream pressure is locked up. They talk a bit about hysteresis on page 5 of the manual. I don't know if you can adjust that hysteresis or not. Again, you'll need to talk to Festo about that because it may present a problem for you. If the pressure to the brake is being increased and for whatever reason it has to be decreased, your control system will be trying to reduce pressure to the brake actuator but it won't change the pressure until you've passed through the hysteresis of this valve and hit the vent set point. Hopefully I've explained that well enough you can understand what you need to look out for.

That brings me to a suggestion. I'm sure this valve isn't very expensive. If you need to model this valve, I'd recommend you simply purchase one and test it. Once you have the valve in hand, you can vary inlet pressure, outlet pressure set point and measure flow. I'd suggest buying a rotometer for measuring flow. I use them all the time and they're very simple and low budget. You may need to explain to your supervisor or whoever, why you need to purchase this regulator and test it, but I think trying to get enough information about how this regulator is going to react from Festo will be an exercise in futility. This is a mass produced valve, so getting that kind of detail out of a manufacturer will be difficult at best. You should just buy one and get the data you need on it. Doing it that way is a lot less expensive than spending hours talking to engineers and sales people at Festo or people like me on the internent. And you'll have much better data than you could possibly get any other way.

 

[serbring]

The regulator's flow rate is a function not only of how far open the poppet is, but also of the upstream and downstream pressures. We can't telll from the graphs, and Festo doesn't tell you, what the upstream pressure is for each of those curves. If the upstream pressure is the same for every curve, I would expect the lower set pressure curves to be out farther to the right than the higher set pressure curves. But that's not the case. It's just the opposite. However, if the upstream pressure is always some small dP above the outlet set pressure, say 1 bar for example, we would expect the curves to look as they do with the higher set pressure curves further out to the right. If you want to understand why that is true, do a calculation on flow through a valve at a fixed Cv and a fixed dP and vary the inlet pressure. You should find that as you increase inlet pressure, flow rate gradually increases. This will give you the red line in your graph that gradually drifts to the right as you increase pressure.

On page 17 of the Festo manual, they have a note next to inlet pressure that says the inlet pressure should always be 1 bar greater than the maximum regulated outlet pressure. I suspect that's where they get the graphs from, the inlet pressure for each of those set pressure lines is for a regulator with an inlet pressure 1 bar above the set pressure. But I can't tell you for sure that's how they came up with those graphs. I realize you want to use these graphs to create your control software and to size things in your system but if you are that concerned about the accuracy of those curves, then at the very least, I'd contact Festo and ask them how they came up with those curves and what the upstream pressure for each line is. If it's 1 bar above the outlet pressure, that won't help you much since your inlet pressure is likely to be significantly higher than 1 bar above set.

Hi Q_Goest,

Thanks for your helpful reply,

I know the maximum flow rate is dependent by the upstream and downstream pressures as well and as I said in one of my previous posts I was a bit suspicious, about the upstream pressure. Therefore few weeks ago I contacted Festo and they said the upstream pressure is the same in any setting condition. I'll try to contact them again.

Regarding the P&ID you sent, I see also that you are assuming this is a self relieving regulator. Looking at the cross section and reading the literature, I believe you're correct. A self relieving regulator actually has 2 valves inside for controlling pressure. It has one that pressurizes the downstream port and one that vents the downstream port when pressure goes too high. In this case, it looks like the Festo regulator vents directly to atmosphere which is a common way to do it. The only other way is to provide a port that a tube or pipe can be connected to in order to vent the gas away. That's commonly done for hazardous gasses such as flammables or toxic gasses.

What you should know is that there's a hysteresis between the pressurization set point (and the one valve opening), and the vent set point (which allows the second valve to open). If you're below the pressurization set point and above the vent set point, both valves are closed and the downstream pressure is locked up. They talk a bit about hysteresis on page 5 of the manual. I don't know if you can adjust that hysteresis or not. Again, you'll need to talk to Festo about that because it may present a problem for you. If the pressure to the brake is being increased and for whatever reason it has to be decreased, your control system will be trying to reduce pressure to the brake actuator but it won't change the pressure until you've passed through the hysteresis of this valve and hit the vent set point. Hopefully I've explained that well enough you can understand what you need to look out for.

Thanks for the hysteresis suggestion, I haven't thought about it so far, mainly because as you know there are many more important things to fix in the model.

That brings me to a suggestion. I'm sure this valve isn't very expensive. If you need to model this valve, I'd recommend you simply purchase one and test it. Once you have the valve in hand, you can vary inlet pressure, outlet pressure set point and measure flow. I'd suggest buying a rotometer for measuring flow. I use them all the time and they're very simple and low budget. You may need to explain to your supervisor or whoever, why you need to purchase this regulator and test it, but I think trying to get enough information about how this regulator is going to react from Festo will be an exercise in futility. This is a mass produced valve, so getting that kind of detail out of a manufacturer will be difficult at best. You should just buy one and get the data you need on it. Doing it that way is a lot less expensive than spending hours talking to engineers and sales people at Festo or people like me on the internent. And you'll have much better data than you could possibly get any other way.

I agree with you and we will do it soon or later but there are many valves in the market and before buying one only because a sales engineer suggested me it, I would prefer to test it by modeling. I don't trust that much to sales engineers. Moreover I'm just a simulation engineer and doing it for a customer that will buy all the hardware.

Regarding the technical drawing, I don't see the pilot stage, where is it? I don't see in the drawing any opening to dome for regulating the pressure, where does the air to the dome come from?

Really thanks for your precious help! :)

Cheers

 

[Q_Goest]

Hi serbring. Interesting comment on the sales engineer. Now I'm wondering; why do you want a regulator? Or why would the sales engineer direct you to that type of valve?

Regulators are used to adjust downstream pressure to a set point. So for an input, they look at pressure. But you're not controlling to pressure, you're controlling to a strain gage. All you want to do is adjust the pressure on the brake so that you get the correct responce from the strain gage. I guess I don't understand why you you have this half way measure of attempting to control pressure. If pressure is too high, your strain gage is sending back a signal that indicates this and your controls will be reducing pressure to adjust.

Could you use a proportional flow control valve instead? Festo makes the http://ftp.festo.com/public/PNEUMATIC/SOFTWARE_SERVICE/PDF_Catalogue/PDF/US/MPYE_ENUS.PDF which might be close to what you need. Looks like it's not a perfect fit but it's very close. It looks like it might be used for an air cylinder without spring return (ie: a double acting cylinder), but I would think you would only want to use the one port on the valve to pressurize the one port on your cylinder. Take a look at the function diagram at the top of page 5. It looks like you would put your supply pressure to port 1, vent port 5 and take port 4 to your cylinder. Ports 2 and 3 would be blocked. With this valve, you measure strain and when it goes high, you vent air pressure and when low you pressurize. There's no hysteresis and no extra controls trying to adjust to a specific pressure. I'm sure there are other valves that would be even better for your application. What I'm wondering though is why you went with a regulator for this application?