westmckay99
- 7
- 0
Hello everyone,
I have a concern regarding the conservation of momentum for an incompressible Newtonian fluid with constant viscosity.
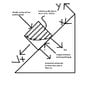
Say you have a volume of fluid sliding down an inclined plane with a velocity Vx with the perpendicular axis facing upward in the y-direction. When you try to solve the set of differential equations for Navier-Stokes in y, you end up with dp/dy=row*g, hence this illustrates the hydrostatic pressure variation. What doesn't make sense is how can a hydrostatic equation for a fluid at rest be applied to a fluid moving? When you derive the hydrostatic balance equation from a simple force balance on an element of fluid you only have 3 forces: Fdown(weight at top surface), Fup(weight at bottom surface), and Fdown(gravity force)... But in our inclined moving fluid system, we should have all the same weight Forces and the y-component of Fg AND also an extra Fdown(due to viscous transportation from the flow in the x-direction). Thus by virtue of this force balance, shouldn't the pressure variation in y be shear stress dependent and not simply a hydrostatic consideration?
I attached a diagram of the situation.
Thanks in advance!
I have a concern regarding the conservation of momentum for an incompressible Newtonian fluid with constant viscosity.
Say you have a volume of fluid sliding down an inclined plane with a velocity Vx with the perpendicular axis facing upward in the y-direction. When you try to solve the set of differential equations for Navier-Stokes in y, you end up with dp/dy=row*g, hence this illustrates the hydrostatic pressure variation. What doesn't make sense is how can a hydrostatic equation for a fluid at rest be applied to a fluid moving? When you derive the hydrostatic balance equation from a simple force balance on an element of fluid you only have 3 forces: Fdown(weight at top surface), Fup(weight at bottom surface), and Fdown(gravity force)... But in our inclined moving fluid system, we should have all the same weight Forces and the y-component of Fg AND also an extra Fdown(due to viscous transportation from the flow in the x-direction). Thus by virtue of this force balance, shouldn't the pressure variation in y be shear stress dependent and not simply a hydrostatic consideration?
I attached a diagram of the situation.
Thanks in advance!