Prime number distribution and hit in a carrom game

[rajeshmarndi]

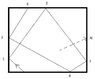
In carrom game, we have black/white small disc pieces, just imagine we have a single piece of it on the board.We hit that pieces with a striker on one side of the four wall. And the pieces goes on hitting side of the wall, number of times.

If I'm right, there cannot be a general formula, which can determine at what point of the wall, the pieces will hit after it goes hitting the wall nth times. We can have a formula, where the hit will be on the next wall but not where the hit will be after the pieces goes through hitting n wall.

What a computer does is, it calculates each hit position and goes on to the next hit position and finally arrive at the nth hit. This is how it can show the nth hit position.

Prime number distribution is similarly. If we take first primes number( for simplicity, ignoring 2 & 3 because we know all 2&3 multiples are not primes) 5,7 11,13 17,19 and 23. All the two combination of these numbers i.e multiply , they will generate composite number(25,35,49,55,65,77,...23^2) and between these composite number are new prime number. Again when these primes number multiply among themselves, they will again generate new composite number and prime number. And this go on.

So, just like we cannot have a formula of the point after nth hit in a carrom, similarly we cannot know nth prime number.

 

[fresh_42]

Not quite sure whether this is a legitimate comparison. The billiard balls are unpredictable because we do not know all parameters for a calculation, it's a lack of information. Prime number distribution was investigated in dozens of papers. Not knowing whether a number is prime or not means we haven't checked, yet. At least we can in principle, even if it takes too long for big primes.