View attachment 4025
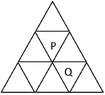
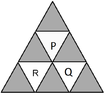
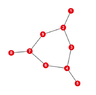
I turned the network of rooms into a graph as in the image by considering the rooms as vertices and numbering them 1 through 9. Room P is vertex number 2 and Q is number 4. Then I made a Markov transition matrix representing the probabilities of going from one room to another.
\[
M=
\left[ {\begin{array}{ccccccccc}
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & 0 & 0 & 0 & \frac{1}{3} \\
0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & \frac{1}{2} & 0 & 0 & 0 & 0 & \frac{1}{2} & 0 & 0 \\
\end{array} } \right]
\]
(Crying)
Then I diagonalized it (with my handy
link, because I refused to do it by hand), took it to the nth power, and I got
\[
M^n = PD^n P^{-1} =
\left[ {\begin{array}{ccccccccc}
1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 \\
-\frac{1}{\sqrt 2} & 0 & \frac{1}{\sqrt 2} & 0 & -1 & 1 & 0 & 0 & 0 \\
0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 \\
\frac{1}{\sqrt 2} & -\sqrt 2 & -\frac{1}{\sqrt 2} & \sqrt{2} & -1 & 1 & 0 & 0 & 0 \\
-1 & 2 & -1 & 2 & 1 & 1 & 0 & 0 & 1 \\
-\frac{1}{2} & 0 & -\frac{1}{2} & 0 & 1 & 1 & 0 & -1 & -1 \\
0 & -2 & 0 & -2 & 1 & 1 & 1 & 2 & 1 \\
0 & \sqrt 2 & 0 & -\sqrt 2 & -1 & 1 & 0 & 0 & 0 \\
\frac{1}{2} & -1 & \frac{1}{2} & -1 & 1 & 1 & -1 & -1 & 0 \\
\end{array} } \right] \times
\]
\[
\left[ {\begin{array}{ccccccccc}
\left (-\frac{1}{\sqrt 2}\right )^n & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \left (-\frac{1}{\sqrt 2} \right )^n & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \left (\frac{1}{\sqrt 2} \right )^n & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \left (\frac{1}{\sqrt 2} \right )^n & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & (-1)^n & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array} } \right] \times
\]
\[
\left[ {\begin{array}{ccccccccc}
\frac{2}{9} & -\frac{\sqrt 2}{3} & \frac{1}{9} & \frac{\sqrt 2}{6} & -\frac{1}{9} & -\frac{2}{9} & -\frac{1}{9} & \frac{\sqrt 2}{6} & \frac{1}{9} \\
\frac{1}{18} & -\frac{\sqrt 2}{12} & \frac{1}{9} & -\frac{\sqrt 2}{12} & \frac{1}{18} & -\frac{1}{18} & -\frac{1}{9} & \frac{\sqrt 2}{6} & -\frac{1}{18} \\
\frac{2}{9} & \frac{\sqrt 2}{3} & \frac{1}{9} & -\frac{\sqrt 2}{6} & -\frac{1}{9} & -\frac{2}{9} & -\frac{1}{9} & -\frac{\sqrt 2}{6} & \frac{1}{9} \\
\frac{1}{18} & \frac{\sqrt 2}{12} & \frac{1}{9} & \frac{\sqrt 2}{12} & \frac{1}{18} & -\frac{1}{18} & -\frac{1}{9} & -\frac{\sqrt 2}{6} & -\frac{1}{18} \\
\frac{1}{18} & -\frac{1}{6} & \frac{1}{9} & -\frac{1}{6} & -\frac{1}{18} & \frac{1}{9} & \frac{1}{18} & -\frac{1}{6} & \frac{1}{9} \\
\frac{1}{18} & \frac{1}{6} & \frac{1}{9} & \frac{1}{6} & \frac{1}{18} & \frac{1}{9} & \frac{1}{18} & \frac{1}{6} & \frac{1}{9} \\
\frac{4}{9} & 0 & -\frac{4}{9} & 0 & \frac{1}{9} & \frac{2}{9} & \frac{1}{9} & 0 & -\frac{4}{9} \\
-\frac{2}{9} & 0 & \frac{5}{9} & 0 & -\frac{2}{9} & -\frac{1}{9} & \frac{1}{9} & 0 & -\frac{1}{9} \\
\frac{1}{9} & 0 & -\frac{4}{9} & 0 & \frac{4}{9} & -\frac{4}{9} & \frac{1}{9} & 0 & \frac{2}{9} \\
\end{array} } \right]
\]
We only want the $ (2,1) $ entry of the resulting matrix, so we only need the diagonal matrix and the second row and fourth column of the $P$ and $ P^{-1} $ matrices, respectively, to find the final matrix (See? I'm stupid-I figured this out only after I multiplied every single entry of the matrices-but I won't show that here). Multiplying, we get
$$ P_{2 \to 4} = \frac{\left ( 1-2^{-n/2} \right ) \Bigl ( (-1)^{n} +1 \Bigr )}{6}, $$
which works for any n, even or odd (it is 0 for odd n, as is clearly seen).