Probability of Reaching Room Q in n Seconds

[jacobi1]

The image shows a network of rooms. A ball starts in room P. If the ball moves from one room to another adjacent one every second (assume no time is spent between the rooms) and it randomly chooses a room to go to, find the probability that it reaches room Q after n seconds. A room is adjacent to another room if and only if they share a side-for example, P is adjacent to three rooms.
View attachment 4010

 

[Opalg]

The image shows a network of rooms. A ball starts in room P. If the ball moves from one room to another adjacent one every second (assume no time is spent between the rooms) and it randomly chooses a room to go to, find the probability that it reaches room Q after n seconds. A room is adjacent to another room if and only if they share a side-for example, P is adjacent to three rooms.

To clarify, do you want the probability that the ball reaches Q for the first time after n seconds, or do you include the possibility that it may also have visited Q previously?

 

[jacobi1]

I include the probability that it may have visited Q previously.

 

[Opalg]

The image shows a network of rooms. A ball starts in room P. If the ball moves from one room to another adjacent one every second (assume no time is spent between the rooms) and it randomly chooses a room to go to, find the probability that it reaches room Q after n seconds. A room is adjacent to another room if and only if they share a side-for example, P is adjacent to three rooms.

[sp]

View attachment 4018​

First, notice that each move of the ball takes it either from a shaded room to an unshaded room, or from an unshaded room to a shaded room. Since rooms P and Q are both unshaded, it is impossible for the ball to go from P to Q in an odd number of moves. So if $n$ is odd, the probability is $0$.

So assume that $n$ is even, and think about the transition probabilities after two moves. The only way to get from P to Q in two moves is to go via the shaded room between them. The probability of going to this shaded room from P is $1/3$, and the probability of then going from the shaded room to Q is $1/2$. So the probability of going from P to Q in two moves is $1/6$. By symmetry, the probability of going from P to R in two moves is also $1/6$. The probability of going from P back to P in two moves is therefore $2/3$ (since the probabilities must add up to $1$). Thus the matrix $T$ giving the transition probabilities between P, Q and R (in two moves) is $$T = \frac16\begin{bmatrix} 4&1&1 \\ 1&4&1 \\ 1&1&4 \end{bmatrix}.$$ Let $I$ denote the $3\times3$ identity matrix, and let $E$ be the idempotent matrix $$E = \frac13\begin{bmatrix} 1&1&1 \\ 1&1&1 \\ 1&1&1 \end{bmatrix}.$$ Then $T = \frac16(3I+3E) = \frac12(I+E)$, and $$T^k = \frac1{2^k}(I+E)^k = \frac1{2^k}\Bigl(I + {k\choose1}E + {k\choose2}E + \ldots + {k\choose k}E \Bigr) = \frac1{2^k}\bigl((2^k-1)E + I\bigr)$$ (using the fact that $E$ is idempotent). The $(2,1)$-element of this matrix is $\dfrac{2^k-1}{3\cdot 2^k}$. Therefore the probability of the ball being in room Q after an even number $n\;(=2k)$ of moves is $\dfrac{2^{n/2}-1}{3\cdot 2^{n/2}}$.[/sp]

 

[jacobi1]

Congratulations, Opalg, your answer is correct. And much faster than mine, too.:)
I did this the hard way. As in, the long, stupid way.

Spoiler

View attachment 4025
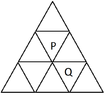
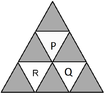
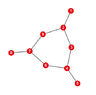
I turned the network of rooms into a graph as in the image by considering the rooms as vertices and numbering them 1 through 9. Room P is vertex number 2 and Q is number 4. Then I made a Markov transition matrix representing the probabilities of going from one room to another.
\[
M=
\left[ {\begin{array}{ccccccccc}
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & 0 & 0 & 0 & \frac{1}{3} \\
0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & \frac{1}{2} & 0 & 0 & 0 & 0 & \frac{1}{2} & 0 & 0 \\
\end{array} } \right]
\]
(Crying)
Then I diagonalized it (with my handy link, because I refused to do it by hand), took it to the nth power, and I got
\[
M^n = PD^n P^{-1} =

\left[ {\begin{array}{ccccccccc}
1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 \\
-\frac{1}{\sqrt 2} & 0 & \frac{1}{\sqrt 2} & 0 & -1 & 1 & 0 & 0 & 0 \\
0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 \\
\frac{1}{\sqrt 2} & -\sqrt 2 & -\frac{1}{\sqrt 2} & \sqrt{2} & -1 & 1 & 0 & 0 & 0 \\
-1 & 2 & -1 & 2 & 1 & 1 & 0 & 0 & 1 \\
-\frac{1}{2} & 0 & -\frac{1}{2} & 0 & 1 & 1 & 0 & -1 & -1 \\
0 & -2 & 0 & -2 & 1 & 1 & 1 & 2 & 1 \\
0 & \sqrt 2 & 0 & -\sqrt 2 & -1 & 1 & 0 & 0 & 0 \\
\frac{1}{2} & -1 & \frac{1}{2} & -1 & 1 & 1 & -1 & -1 & 0 \\
\end{array} } \right] \times
\]

\[
\left[ {\begin{array}{ccccccccc}
\left (-\frac{1}{\sqrt 2}\right )^n & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \left (-\frac{1}{\sqrt 2} \right )^n & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \left (\frac{1}{\sqrt 2} \right )^n & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \left (\frac{1}{\sqrt 2} \right )^n & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & (-1)^n & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array} } \right] \times
\]

\[
\left[ {\begin{array}{ccccccccc}
\frac{2}{9} & -\frac{\sqrt 2}{3} & \frac{1}{9} & \frac{\sqrt 2}{6} & -\frac{1}{9} & -\frac{2}{9} & -\frac{1}{9} & \frac{\sqrt 2}{6} & \frac{1}{9} \\
\frac{1}{18} & -\frac{\sqrt 2}{12} & \frac{1}{9} & -\frac{\sqrt 2}{12} & \frac{1}{18} & -\frac{1}{18} & -\frac{1}{9} & \frac{\sqrt 2}{6} & -\frac{1}{18} \\
\frac{2}{9} & \frac{\sqrt 2}{3} & \frac{1}{9} & -\frac{\sqrt 2}{6} & -\frac{1}{9} & -\frac{2}{9} & -\frac{1}{9} & -\frac{\sqrt 2}{6} & \frac{1}{9} \\
\frac{1}{18} & \frac{\sqrt 2}{12} & \frac{1}{9} & \frac{\sqrt 2}{12} & \frac{1}{18} & -\frac{1}{18} & -\frac{1}{9} & -\frac{\sqrt 2}{6} & -\frac{1}{18} \\
\frac{1}{18} & -\frac{1}{6} & \frac{1}{9} & -\frac{1}{6} & -\frac{1}{18} & \frac{1}{9} & \frac{1}{18} & -\frac{1}{6} & \frac{1}{9} \\
\frac{1}{18} & \frac{1}{6} & \frac{1}{9} & \frac{1}{6} & \frac{1}{18} & \frac{1}{9} & \frac{1}{18} & \frac{1}{6} & \frac{1}{9} \\
\frac{4}{9} & 0 & -\frac{4}{9} & 0 & \frac{1}{9} & \frac{2}{9} & \frac{1}{9} & 0 & -\frac{4}{9} \\
-\frac{2}{9} & 0 & \frac{5}{9} & 0 & -\frac{2}{9} & -\frac{1}{9} & \frac{1}{9} & 0 & -\frac{1}{9} \\
\frac{1}{9} & 0 & -\frac{4}{9} & 0 & \frac{4}{9} & -\frac{4}{9} & \frac{1}{9} & 0 & \frac{2}{9} \\
\end{array} } \right]
\]
We only want the $ (2,1) $ entry of the resulting matrix, so we only need the diagonal matrix and the second row and fourth column of the $P$ and $ P^{-1} $ matrices, respectively, to find the final matrix (See? I'm stupid-I figured this out only after I multiplied every single entry of the matrices-but I won't show that here). Multiplying, we get
$$ P_{2 \to 4} = \frac{\left ( 1-2^{-n/2} \right ) \Bigl ( (-1)^{n} +1 \Bigr )}{6}, $$
which works for any n, even or odd (it is 0 for odd n, as is clearly seen).

 

[Opalg]

I did this the hard way.

Confession: I also started by writing down a $9\times9$ matrix. But then I thought: that looks impossibly hard, there must be an easier way. (Headbang) (Emo)