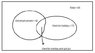
Saracen Rue
- 150
- 10
Homework Statement
During the Christmas holidays, 42 students from a group of 85 students found vacation employment while 73 students went away for holidays. Assuming that every student had at least a job or went on a holiday, what is the probability that a randomly selected student worked through the holidays (that is, did not go away on holidays), given that he/she had a job.
Homework Equations
I'm not sure if all of these are needed for this specific question, but I'm going to post every equation I was given just in case:
- Pr(A) = Pr(A|B)Pr(B) + Pr(A|B')Pr(B')
- Pr(A) = Pr(A∩B) + Pr(A∩B')
- Pr(A|B) = Pr(A∩B)/Pr(B)
- Pr(A∪B) = Pr(A) + Pr(B) - Pr(A∩B)
- Pr(A∪B) = n(A∪B)/n(http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i1/s4univ.gif)
The Attempt at a Solution
First, I wrote out the information I knew;
n(http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i1/s4univ.gif) = 85
A = students who worked = 42
B = students who went away = 73
Pr(A) = 42/85
Pr(B) = 73/85
Next, I solved for Pr(A∪B):
Pr(A∪B) = n(A∪B)/n(http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i1/s4univ.gif)
Pr(A∪B) = 115/85
I then attempted to plug 115/85 into the equation Pr(A∪B) = Pr(A) + Pr(B) - Pr(A∩B) and solve for Pr(A∩B), but I encountered a problem...
Pr(A∪B) = Pr(A) + Pr(B) - Pr(A∩B)
115/85 = 42/85 + 73/85 - Pr(A∩B)
115/85 = 115/85 - Pr(A∩B)
0 = Pr(A∩B)
As you can see, using the equation results in Pr(A∩B) = 0. However, I know this cannon be true as A+B > n(http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i1/s4univ.gif).
So, I tried to just use common sense to determine Pr(A∩B); I added A and B together and took away n(http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i1/s4univ.gif). This left me with Pr(A∩B) = 30/85. I then used this to determine that Pr(A∩B') = 12/85 (by taking 30 away from A) and Pr(A'∩B) = 43/85. From here, I decided to attempt to solve the actual equation, which I believed would use the equation Pr((A∩B')|A).
Pr(A|B) = Pr(A∩B)/Pr(B)
Pr((A∩B')|A) = Pr((A∩B')∩A)/Pr(A)
Now, I needed to find Pr((A∩B')∩A), but to do that I needed to know Pr((A∩B')∪A).
Pr((A∩B')∪A) = n((A∩B')∪A)/n(http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i1/s4univ.gif)
Pr((A∩B')∪A) = 12+42/85
Pr((A∩B')∪A) = 54/85
Next, I tried to use the equation Pr(A∪B) = Pr(A) + Pr(B) - Pr(A∩B) again, but the same thing happened...
Pr(A∪B) = Pr(A) + Pr(B) - Pr(A∩B)
Pr((A∩B')∪A) = Pr(A∩B') + Pr (A) - Pr((A∩B')∩A)
54/85 = 12/85 + 42/85 - Pr((A∩B')∩A)
54/85 = 54/85 - Pr((A∩B')∩A)
0 = Pr((A∩B')∩A)
As you can see, this formula once again resulted giving me an answer of 0. I also just can't solve this with common sense as it's getting too complicated for me to actually understand what's going on. I think that there's something wrong with this formula, so if anyone could fix it or give me a correct one it would be much appreciated.
Also, I'm sorry if this is really obvious and I'm just being an idiot. I'm good at most areas of maths but for some reason I always struggle immensely with probability... anyway, thank you all for taking the time to read this.