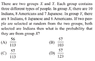Probability that both people are from group X

[jaus tail]

Homework Statement

Homework Equations

Probability = number of favourable events / all possible events

The Attempt at a Solution

Group X Y Total people
Indians 10 8 18 (total 18 Indians in both group)
Total People 25 20 45 (total 45 people in both group combined)

Both selected people are Indians.
There are 3 cases.
One: Both Indians are from group X.
Two: Both Indians are from group Y.
Three: One Indian is from X, other is from Y.
Probability of each is 1/3

Three cases
Case one i.e. both are from group X: 10C2 / 25C2 = 0.15
Case two i.e both are from group Y: 8C2 / 20C2 = 0.147
Case three i.e one from X, one from Y: 10C1 * 8C1 / [ 25C1 * 20C1 ] = 0.16

So answer is: 0.15 / [ (1/3) (0.15 + 0.147 + 0.16) ] = 0.985 which doesn't match any of the options.

 

[StoneTemplePython]

key question: can one person be selected twice? I.e. are they sampling with or without replacement?

Also, did you try drawing a tree? A picture would be quite helpful. It should be a Bayes problem, but I'm not sure on replacement.

another idea would be to draw a state diagram / directed graph and try to set this up as a Markov chain.

 

[StoneTemplePython]

Both selected people are Indians.
There are 3 cases.
One: Both Indians are from group X.
Two: Both Indians are from group Y.
Three: One Indian is from X, other is from Y.
Probability of each is 1/3

Where did the $\frac{1}{3}$ come from? What if group $X$ was all Indians (with same total number of people), but group $Y$ had only $2$ Indians (and same total number of people). Would you still say $\frac{1}{3}$? What if group $Y$ only had 1 or zero Indians?

 

[jaus tail]

1/3 is probability that people are selected from group X, since there are only 3 cases.
Yeah the sampling confused me as well. I tried with all sampling possibilities but didn't get answer.
You're right that this is Baye's problem as the solved examples before this are of Baye's type and they've used urns in that.

 

[StoneTemplePython]

Let's try an easier problem:

Urn $X$ has 10 balls, 4 are green and 6 are red. Urn $Y$ has 10 balls, 7 of which are green and 3 are red. Let's solve these two cases:
- - - -
1.) Suppose I pick one ball and get a green. Whats the probability I drew it from urn $X$?

2.) Now suppose I pick one ball -- its green. Then I put that ball into my pocket. I draw another ball from an undisclosed urn, and that is green too. What's the probability they both came from urn $X$?
- - - -
Also, I seem to think you code -- if I'm wrong then disregard this. Have you tried coding and then running a simulation? I find that they can help build 'physical intuition' for these problems.

 

[jaus tail]

How to type fractions: I'm typing latex code but it's not working \frac a b

Anyway for 1st question:
Urn X has 4 green and 6 red
Urn Y has 7 green and 3 red

Pick one ball and it's green, so total number of cases are (ball from Urn X and it's green) + (ball from Y and it's green)
which is (1/2 times 4/10 + 1/2 times 7/10) which is 0.55

And favourable case is ball is from X so it's (1/2 times 4/10) which is 0.2
So answer is 0.2 divide by 0.55 = 0.3636
Right?

 

[jaus tail]

For second question:

Urn X has 4 green and 6 red
Urn Y has 7 green and 3 red

Two balls are taken. Both are green. Probablity that both are from X
There are 4 cases. Balls are taken from (X,X ; X,Y ; Y,X ; Y,Y)
Probability of each case is 1/4
And we know that both balls are green. So total number of cases is
(1/4)(4C2 / 10C2) + (1/4)(4/10 * 7/10) + (1/4)(7/10 * 4/10) + (1/4)(7C2 / 10C2)
Which gives 0.29

And favorable case is (X,X) which is (1/4)(4C2 / 10C2) = 0.033

I've done something wrong somewhere. Favourable cases can't be more than total number of cases.

 

[StoneTemplePython]

For Latex,

1.) check out the sticky here: https://www.physicsforums.com/help/latexhelp/
-- a key idea is to surround your latex with double hashtags on each side like #\frac{a}{b}# except double hashtags like $\frac{a}{b}$
2.) check this out: http://www.codecogs.com/latex/eqneditor.php
3.) you can right click the latex in my posts and select "show math as" -> "tex commands" to see the commands I used.

- - - -
so for this simpler problem,
there are 4 greens in X, 7 in Y and 20 balls total. So probability of drawing a ball that is green is $\frac{11}{20}$ this is our denominator. Probability of drawing a green from $X$ is $\frac{4}{20}$. This gives $\frac{\frac{4}{20} }{ \frac{11}{20}} = \frac{4}{11}$

There's an even simpler reduced sample space approach, but I'm thinking I don't want to go there.

Do you understand the above? I think you're trying to chain in a prior probability that you shouldn't be... Drawing a picture like a tree should be quite helpful. And from there you'd just be chaining on more binary trees.

Let's get this Case 1 locked down before moving on to Case 2.

 

[jaus tail]

We both got right answer. Lol.
But why did you combine the urns? I didn't understand how you can do that.

 

[jaus tail]

So then as per your route for second case we have:
probability of drawing both green from Urn X is ⁴C₂₀
And for denominator we have ¹¹C₂₀
Dividing them we get:
\frac{⁴C₂₀}{¹¹C₂₀} = 0.109
Still not getting fraction

\frac{a}{b}

 

[StoneTemplePython]

Ha. I didn't even realize they matched (up to truncating the repeated decimal).

The key idea, is to really focus on the sampling mechanism. (And if you code it forces you to do this when you are coding up the simulation.)

For Case 1:

The way I'd think about this is: you are watching someone (me) draw a ball from urns, except this is being done in a different room / under the table, etc. so you can't see which urn I reach into. I just show you the green ball at the end. From your vantage point, this is the same as if I reach into one big combined urn and then you need to work backward to reason which urn I most likely reached into.

Thus your first interest is info like the total probability of drawing a green ball, period. Then you want to partition things and look into total probability of drawing a green ball that is from $X$ and total probability of drawing a green ball from $Y$.

Does this line up with how you think about it?

 

[jaus tail]

Okay got it. And for second one. Is my answer correct there?

 

[jaus tail]

I think I've done wrong for second case
there are 4 greens in X, 7 in Y and 20 balls total.
2 balls are taken and both are green and we have to find P(both are from X)
So numerator is 4C2 / 20C2 which is 0.0316
Denominator is 11C2 / 20C2 which is 0.29

Numerator / denominator = 0.109

 

[StoneTemplePython]

So then as per your route for second case we have:
probability of drawing both green from Urn X is ⁴C₂₀
And for denominator we have ¹¹C₂₀
Dividing them we get:
\frac{⁴C₂₀}{¹¹C₂₀} = 0.109
Still not getting fraction

\frac{a}{b}

try double hash tags around your latex. Also, try using that code cogs link -- it would give you a different way of doing binomial like this $\binom{20}{4}$
- - - -
I get the same result.

In the interest of not skipping steps, I did enumeration.
- - - -
total probability of those 2 greens is:

$\frac{11}{20}\frac{10}{19} = \frac{110}{19*20}$

we can partition this into

probability both greens from X
$\frac{4}{20}\frac{3}{19} =\frac{12}{20*19}$

probability one green from X and one from Y
$\frac{4}{20}\frac{7}{19} + \frac{7}{20}\frac{4}{19} = 2 \big(\frac{4}{20}\frac{7}{19}\big)$

probability both greens from Y
$\frac{7}{20}\frac{6}{19}$

note: a good check that the partition is correct is to add them all up (i.e. calculating the same thing two different ways and having the results agree is a very smart maneuver in probability.)

$\frac{4}{20}\frac{3}{19} + 2 \big(\frac{4}{20}\frac{7}{19}\big) + \frac{7}{20}\frac{6}{19} = \frac{110}{20*19}$

so this checks out.
- - - -

hence the probability of interest is

$\frac{\frac{12}{20*19}}{ \frac{110}{20*19}} = \frac{12}{110} = \frac{6}{55} \approx 0.109$

 

[StoneTemplePython]

I think I've done wrong for second case
there are 4 greens in X, 7 in Y and 20 balls total.
2 balls are taken and both are green and we have to find P(both are from X)
So numerator is 4C2 / 20C2 which is 0.0316
Denominator is 11C2 / 20C2 which is 0.29

Numerator / denominator = 0.109

You have the same (correct) result here. This is how I'd do it using combinations, though there is value in enumeration for the small problems.

 

[jaus tail]

Thanks. I guess there is some typo in original question as I'm not getting any answer that matches options.
Thanks for fraction help as well
$\frac{a}{b}$

 

[StoneTemplePython]

Thanks. I guess there is some typo in original question as I'm not getting any answer that matches options.
Thanks for fraction help as well
$\frac{a}{b}$

I'm getting $\frac{15}{51}$ which is not one of the available answers...

 

[jaus tail]

Yup even I'm getting $\frac{5}{17}$ which is same as ur answer.
Here is how I did:
Group X has 10 Indians and total 25 people
Group Y has 8 Indians and total 20 people
Total there are 18 Indians and 45 people.
2 people selected are Indians.
Denominator is $\frac{18C2}{45C2}$

2 Indians from group X
Numerator is
$\frac{10C2}{45C2}$

$\frac{Num}{Den}$
Which gives answer.

 

[Ray Vickson]

Yup even I'm getting $\frac{5}{17}$ which is same as ur answer.
Here is how I did:
Group X has 10 Indians and total 25 people
Group Y has 8 Indians and total 20 people
Total there are 18 Indians and 45 people.
2 people selected are Indians.
Denominator is $\frac{18C2}{45C2}$

2 Indians from group X
Numerator is
$\frac{10C2}{45C2}$

$\frac{Num}{Den}$
Which gives answer.

Alternative solution: we have 18 Indians --- 10 from X and 8 from Y. Select two Indians without replacement. The probability they both come from X is $10/18 \times 9/17 = 5/17.$