Problem finding exterior angle

  • Thread starter Thread starter 1/2"
  • Start date Start date
  • Tags Tags
    Angle
Click For Summary

Homework Help Overview

The problem involves a triangle ABC inscribed in a circle, with specific angles given and a request to find angle DAC. The context includes geometric properties related to inscribed angles and arcs.

Discussion Character

  • Exploratory, Assumption checking, Conceptual clarification

Approaches and Questions Raised

  • The original poster attempts to calculate angle BAC and uses properties of inscribed angles but struggles to progress further. Some participants suggest using the theorem regarding opposite angles in inscribed quadrilaterals, while others express confusion about the original poster's understanding of the problem.

Discussion Status

The discussion includes attempts to clarify the application of geometric theorems and the original poster's request for more direct guidance. There is an indication that some participants are exploring different interpretations of the problem, but no consensus has been reached.

Contextual Notes

The original poster mentions a diagram from a book, which may not be clear, and there is a reference to an answer provided in the book that may not align with the discussion. This could indicate potential constraints in understanding the problem setup.

1/2"
Messages
98
Reaction score
0

Homework Statement


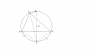
Triangle ABC has been inscribed in the circle with center o.E is the midpoint of arc BC.DE is the diameter.E is joined to A, B and C.D is joined to A . If angle ABC =72 degrees and angle ACB = 48 degrees,
find angle DAC.
(I have attached the diagram given in book although its not a very good one)

Homework Equations


-

The Attempt at a Solution


In this one what i did was,
i found angle BAC =(180-72-48)= 60 degrees
then i tried to subtend angle from the diameter to get 90 degree on the circumference but it did not help.
and i found the other angles like angle BEA=48 degrees and angle DEC= 72 degrees by the theorem the a chord extend equal angles on the circumference. But i can't get any further than this .Please help.
the answer given in my book is 60 degrees.
If I am going wrong somewhere please do let me know.
Thank you.
 

Attachments

  • Untitled.png
    Untitled.png
    2.4 KB · Views: 445
Physics news on Phys.org
hi 1/2"! :smile:

use the theorem that opposite angles subtended from the same chord (ie opposite angles of an inscribed quadrilateral) add up to 180° :wink:
 
I think i have already done it.
can you please be alittle more elaborate?
thanks.:smile:
 
1/2" said:
I think i have already done it.
can you please be alittle more elaborate?
thanks.:smile:

i'm confused … if you've already done it, what's the problem?

and I've given you the full theorem … what is there to elaborate further? :confused:
 
I am really sorry to confuse you.:frown:
Could you give a more direct clue how to get the angle DAC?
and i am really sorry.
 
Thank you
but i have got it.
 

Similar threads

What is the exterior angle of a triangle?
  • · Replies 15 ·
Replies
15
Views
2K
Geometric Reasoning: Find Angle ABC in Rhombus ABDF
  • · Replies 24 ·
Replies
24
Views
2K
Euclidean and non Euclidean geometries problems
  • · Replies 4 ·
Replies
4
Views
4K
Portion of Altitude of a Triangle Inscribed in a Circle
  • · Replies 9 ·
Replies
9
Views
4K
How Do You Calculate the Distance Between Adjacent Numbers on a Clock Face?
  • · Replies 2 ·
Replies
2
Views
2K
How Can I Solve These Precalculus Problems Involving Angles?
  • · Replies 2 ·
Replies
2
Views
2K
Finding Triangle Angles with Cosine Rule
  • · Replies 5 ·
Replies
5
Views
2K
Finding the angle for force component
  • · Replies 1 ·
Replies
1
Views
3K
Finding the Ratio of Angles of Tree A & B
  • · Replies 6 ·
Replies
6
Views
4K
Prove the angles equal to prove the sides triangle problem
  • · Replies 8 ·
Replies
8
Views
3K