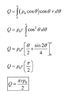I Problem understanding the shear force integral.

[FabledIntg]

The problem is to determine the shearforce Q on the hut near the ground. This is not a homework or anything like that, I'm just studying for an exam and this problem is in the book "Engineering Mechanics, Statics" By Meriam Kraige.

On another forum, I found this:

I understand the part in the parenthesis in the first integral, it's just the all the horizontal components of P summed. But why multiply with r? And why go from 0 to π when the wind only generates pressure against the right side of the hut, which goes from 0 to π/2?

 

[Orodruin]

But why multiply with r?

It is part of the surface element on the hut. The force on a small surface element is $-p \, d\vec S$, where $d\vec S$ is the directed surface element.

Note that the force quoted is the force per length in the direction that goes into the image. (Note that the units do not match otherwise.)

And why go from 0 to π when the wind only generates pressure against the right side of the hut, which goes from 0 to π/2?

This is not true. There is an overpressure generated on the right side but there is an underpressure generated on the left side. This leads to an absence of force in the direction to the right relative to the case where the pressure is homogeneous.

 

[FabledIntg]

So what is $d\vec{S}$? How do you go from $d\vec{S}$ to $d\theta$?

Seems LaTeX doesn't work like this.

 

[Orodruin]

As usual in vector calculus.
$$
\newcommand{\dd}[2]{\frac{\partial #1}{\partial #2}}
d\vec S = \dd{\vec x}{\theta} \times \dd{\vec x}{z} d\theta \, dz
$$
since the cabin surface is a half cylinder that can be parametrised by $\theta$ and $z$ ($z$ being the direction into the image). This evaluates to
$$
d\vec S = \vec e_r r\, d\theta\, dz.
$$
Since you are looking at the force per length, the $dz$ is the corresponding length in the $z$ direction that you need to divide by.

 

[FabledIntg]

Okay thanks for your answers. But we haven't learned parametrisation of surfaces yet. Is there another way of solving this problem with rectangular coordinates?

 

[Orodruin]

Just consider a small surface between $\theta$ and $\theta + d\theta$. The area of that surface is clearly $r\, d\theta \, dz$. The force is in the normal direction of the surface, which gives you a cosine for the component in the $x$-direction (the other cosine comes from the pressure variation itself).

 

[FabledIntg]

I really don't see how the area is clearly r*dθ*dz. I suppose you're referring to the surface area of the body, and not the side where the windows of the hut are. If I choose an are that is generated by going from θ to dθ, The surface area is the circumference from θ and dθ multiplied by the length of the hut in z-direction.

 

[Orodruin]

I suppose you're referring to the surface area of the body, and not the side where the windows of the hut are.

Yes, this is where the force is acting.

The surface area is the circumference from θ and dθ multiplied by the length of the hut in z-direction.

So what is the length of the circle element going from $\theta$ to $\theta + d\theta$?
Note! It is from $\theta$ to $\theta + d\theta$ - not $\theta$ to $d\theta$!

 

[FabledIntg]

Ah, I see now. That should be r*dθ. The x-component of P is P_x = P₀*cos²(θ). Do I now need to sum all of these x-components?

 

[Orodruin]

Yes, which is just performing the original integral.

 

[FabledIntg]

But I'm essentially multiplying r*dθ*L with P₀*cos^2(θ), and then integrating from 0 to π. Can you explain why I have to do this multiplication? What does it mean in a physical sense? Multiplying an infinitesimal area with a force.

 

[Orodruin]

Because the force is the area times the pressure so the force on the area element you just described is $-p \vec e_r r \, d\theta\, L$, where $\vec e_r$ is the unit normal of the roof. The pressure is $p_0 \cos(\theta)$, the other cosine - as already stated - comes from taking the component of the force in the $x$-direction.

 

[FabledIntg]

Perfect! I understand now! One last thing, why did you choose to have the force negative? Is it simply because the x-axis is negative if going to the left, and y-axis negative if going down?

 

[Orodruin]

Because the pressure force on the roof from the outside is in the opposite direction of the surface normal if it is chosen to point out of the roof (the pressure force points into the roof).

 

[FabledIntg]

Great, thank you for your help sir!