Amaelle
- 309
- 54
- Homework Statement
- look at the image
- Relevant Equations
- Stocke theorem!
Greetings!
The exercice ask to calculate the circuitation of the the vector field F on the border of the set omega
I do understand the solution very well
my problem is the region!
I m used to work with a region delimitated clearly by two intersecting function here the upper one stop a y=3 and doesn´t intersect with y=0.
thank you!
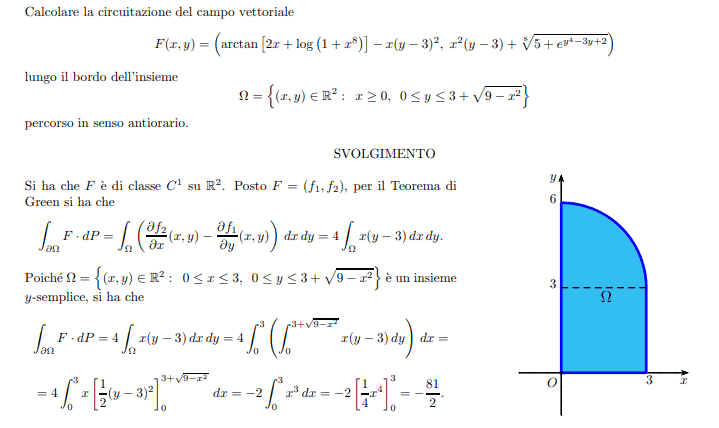
The exercice ask to calculate the circuitation of the the vector field F on the border of the set omega
I do understand the solution very well
my problem is the region!
I m used to work with a region delimitated clearly by two intersecting function here the upper one stop a y=3 and doesn´t intersect with y=0.
thank you!