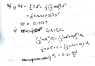You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Problems calculating the New Moment of Inertia
- Thread starter KMconcordia
- Start date
AI Thread Summary
The discussion focuses on calculating the new moment of inertia (MoI) after adding a mass to a rotating disc. Two main approaches are suggested: finding the center of mass (C.O.M) of the system or applying conservation of angular momentum about a fixed point. It is emphasized that the new C.O.M changes with the added mass, affecting the MoI calculation. The importance of considering the mass of the attached object in relation to the disc's mass is highlighted, as it influences the new center of rotation. The correct method involves calculating the new C.O.M and then applying conservation of angular momentum to find the updated MoI.
Physics news on Phys.org
- 42,708
- 10,459
There are a couple of ways to approach this problem.
You can find the mass centre of the system then use that angular momentum will be conserved about that point. I tend to avoid finding mass centres of systems because there is usually an easier way, but in this case it might be simplest.
Alternatively, you can take conservation of angular momentum about any fixed point - the initial position of either the centre of the disc or the point where the mass is attached, say. This way, you can just treat each body as contributing to angular momentum, but you will also need to use conservation of linear momentum. E.g. if you take the initial position of the disc's centre as axis then the subsequent linear motion of the attached particle needs to be related to the new angular rotation rate.
Your calculation of the new MoI is in respect of an axis at the perimeter of the disc. That would be fine if that point were the new centre of rotation, but it will not be. The mass of the attached object must feature in the answer. E.g. if the attached mass is very small there will be little change to the rotation of the disk.
You can find the mass centre of the system then use that angular momentum will be conserved about that point. I tend to avoid finding mass centres of systems because there is usually an easier way, but in this case it might be simplest.
Alternatively, you can take conservation of angular momentum about any fixed point - the initial position of either the centre of the disc or the point where the mass is attached, say. This way, you can just treat each body as contributing to angular momentum, but you will also need to use conservation of linear momentum. E.g. if you take the initial position of the disc's centre as axis then the subsequent linear motion of the attached particle needs to be related to the new angular rotation rate.
Your calculation of the new MoI is in respect of an axis at the perimeter of the disc. That would be fine if that point were the new centre of rotation, but it will not be. The mass of the attached object must feature in the answer. E.g. if the attached mass is very small there will be little change to the rotation of the disk.
KMconcordia
- 6
- 0
So which formula would be the correct way to approach part B?
- 42,708
- 10,459
It's not a matter of some handy formula readily applied. You must first decide your approach. I described two options.KMconcordia said:So which formula would be the correct way to approach part B?
Delta2
Homework Helper
- 6,002
- 2,628
@haruspex you say something about using conservation of linear momentum... I tried to read the problem as carefully as I could but I couldn't find any data regarding the linear momentum of any of the bodies, isn't the linear momentum 0 for all bodies of the system (before and after the "collision")?
Last edited:
- 42,708
- 10,459
The system has zero linear momentum throughout, but after the collision they will each have linear momentum.Delta2 said:@haruspex you say something about using conservation of linear momentum... I tried to read the problem as carefully as I could but I couldn't find any data regarding the linear momentum of any of the bodies, isn't the linear momentum 0 for all bodies of the system (before and after the "collision")?
KMconcordia
- 6
- 0
Do you have any other way in mind about approaching this problem? My final exams tomorrow and I am very lost..Delta2 said:@haruspex you say something about using conservation of linear momentum... I tried to read the problem as carefully as I could but I couldn't find any data regarding the linear momentum of any of the bodies, isn't the linear momentum 0 for all bodies of the system (before and after the "collision")?
Delta2
Homework Helper
- 6,002
- 2,628
Calculate the C.O.M of the disk+particle, then find the moment of inertia ##I'## of disk+particle around the C.O.M, then apply conservation of angular momentum ##I'\omega'=I\omega##
Delta2
Homework Helper
- 6,002
- 2,628
b) would be approximately correct if the mass of 10kg was small compared to the mass of the disc so that the new center of rotation was about the same as the old center of rotation and the same as the center of the disc. But 10kg is a lot compared to the 0.5kg of the mass of the disc so this method isn't correct all.
As i said before you have to find the new c.o.m of the system which will be the new center of rotation. That's the tricky part of this exercise, that the center of rotation changes (and the center of mass as well) when the mass of 10kg is added to the disc.
To find the new c.o.m of the system: Imagine that you have a mass of 0.5kg as a point particle at the center, and the mass of 10kg at distance R=0.25m, then the c.o.m is at distance x from the center such that ##0.5x-10(R-x)=0##. Then calculate the total moment of inertia around the new c.o.m and then use conservation of angular momentum.
EDIT: I had a small mistake in the equation regarding the new c.o.m of the system which i corrected.
As i said before you have to find the new c.o.m of the system which will be the new center of rotation. That's the tricky part of this exercise, that the center of rotation changes (and the center of mass as well) when the mass of 10kg is added to the disc.
To find the new c.o.m of the system: Imagine that you have a mass of 0.5kg as a point particle at the center, and the mass of 10kg at distance R=0.25m, then the c.o.m is at distance x from the center such that ##0.5x-10(R-x)=0##. Then calculate the total moment of inertia around the new c.o.m and then use conservation of angular momentum.
EDIT: I had a small mistake in the equation regarding the new c.o.m of the system which i corrected.
Last edited:
Similar threads
- Replies
- 11
- Views
- 1K
- Replies
- 40
- Views
- 5K
- Replies
- 2
- Views
- 2K
- Replies
- 13
- Views
- 3K
- Replies
- 6
- Views
- 946
- Replies
- 28
- Views
- 1K
- Replies
- 25
- Views
- 2K
- Replies
- 5
- Views
- 3K
- Replies
- 4
- Views
- 2K
- Replies
- 9
- Views
- 2K
Hot Threads
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math