Problems in understanding kinematics

[arifle]

TL;DR

wheeled robot kinematics and constraints

Hi, I tried to understand kinematics after having an omnidirectional roobt. Some problems stop me to go further. Here I upload some contents of different papers talking about kinematics. For the 1st three pictures, I don't know how equation (8) is from and I am little confused about translational and tangentianal velocities. I don't know why it mutiplys R(theta) again in equation (8).

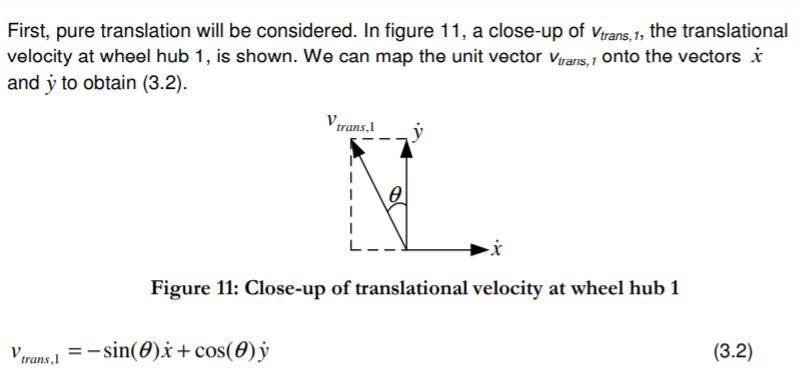
For the 2nd paper, I cannot obtain the equation of v_trans,i. Also, I am not sure if the rotation matrix in this case is R(theta) = [cos(theta) -sin(theta); sin(theta) cos(theta)]. Can anyone please tell some details about the kinematics.

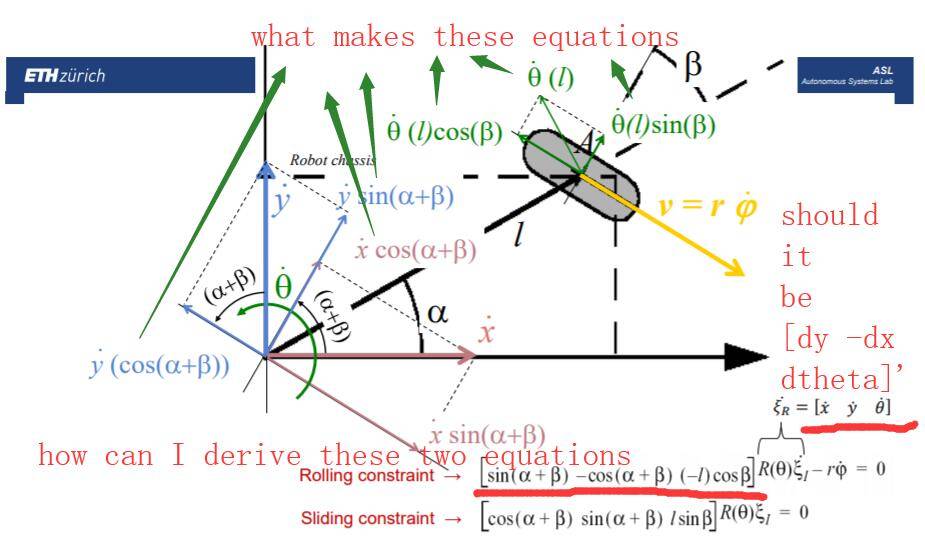
At last, there is another lecture about kinematics. The problem is still about the constraints. How can I derive this pure rolling constraint.

 

[tnich]

It looks to me as though equation (8) in the first paper is the dot product of the drive velocity with the direction vector of the drive's wheel, i.e. the component of the velocity in the direction of the wheel spins. I guess that would imply that the wheel is also sliding sideways. If $\theta$ is a function of time, then the extra multiplication by $\mathbf R(\theta(t))$ would give the direction of the wheel at time $t$.

 

[arifle]

It looks to me as though equation (8) in the first paper is the dot product of the drive velocity with the direction vector of the drive's wheel, i.e. the component of the velocity in the direction of the wheel spins. I guess that would imply that the wheel is also sliding sideways. If $\theta$ is a function of time, then the extra multiplication by $\mathbf R(\theta(t))$ would give the direction of the wheel at time $t$.

Thank you, tnich. How can we get the equation of the rolling constraint if we focus on the 3rd approach.