Prog Simulation: Force of spring across time intervals

[Selroth]

Hello again. Still trying my hand at a physics simulation, as I've been re-learning a lot of forgotten physics and math in my journey! Been stuck on this problem for a few days now though, and thought I'd consult the experts! I'm probably missing something obvious, and the solution is simple...

My "game engine" executes bits of code each frame to find all the forces acting on a particle. Each force has its own code function. I've done well with constant forces (acceleration) such as gravity, and am sure I understand how to implement non-constant forces.

However, I'm having trouble with a non-constant force that depends on the particle's position: a spring.

At time t, the velocity and position of the particle are known. dt (delta time, the time interval between frames) is a forecast of time that will pass. I need to find the average force exerted between t and t + dt.

However, to evaluate the force of a spring, we need to know the object's (particle's) position at the time of evaluation. But, we don't know the particle's position for any time > t.

Is there any other way to figure, accurately, the average force a spring will exert between two instances of time? I know the object's acceleration and position at time t. I also know the object's mass and velocity, thus its kinetic energy. Anything after t is unknown - I just know how much time will pass.

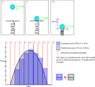
I've attached some notes I drew up to help visualize the problem. The green box is the implementation I'm after, thus I'd need to find the definite integral of the spring's force between t and t + dt. But, I can't because the spring's force is a function of -k*x, and x is unknown.

 

[CompuChip]

You say that at time t, you know the position of the particle (x) and its velocity (v).
So then can't you estimate the position at time t + dt as x + v dt?

 

[Selroth]

You say that at time t, you know the position of the particle (x) and its velocity (v).
So then can't you estimate the position at time t + dt as x + v dt?

If the spring had no impact on the particle, then x + v*dt would be accurate. However, the spring would add resistance, thus the position would be less than that.

 

[Selroth]

Bump? I was afraid of only getting one reply...

 

[Selroth]

Programming a spring

I'm still having a lot of trouble programming a spring in my basic simulation. I'm sure the solution is staring me in the face, mocking me.

Consider the following code:

myMass = 1;
myAcc = 0; 
myVel = 0;
myPos = 20; //20 pixels from the top border

myGravity = -10;
mySpringStart = 90; //The spring begins at 90 pixels, and extends to the bottom.  
mySpringConstant = 0.5 //Arbitrary spring constant number.

do{
	dt = 10; //10 miliseconds

	if (myPos > mySpringStart){
		//Hooke's spring equation: F = -kx
		myForce = mySpringConstant * (myPos - mySpringStart);
	}else{
		myForce = 0;
	}
	
	//Acc = Force/Mass
	myAcc = 0;
	myAcc = myAcc + myForce / myMass;
	myAcc = myAcc + myGravity / myMass;
	
	//Pf = Pi + Vi*t + (Acc*t^2)/2
	//Vf = Vi + Acc*t
	myPos = myPos + myVel*dt + (myAcc*dt*dt)/2; 
	myVel = myVel + myAcc * dt;
	
	draw();
}while(true);

The above code yields a blue graph similar to the one I've drawn and attached. The simulated force is not accurate, and it is delayed by one time interval. I understand I'd need to take the definite integral (between t and t+dt) of the spring function, but that requires me to know the future position of the ball since a spring is a function of position. Yet, I don't have the future position - in fact, the entire engine is based on finding the position.

Does anyone have any advice for me? I'll be watching this topic, and appreciate multiple replies (I'm tired of having 1 reply after all this work posting, then no one ever looking at the thread again because it's "replied" to). I really appreciate any insight!

 

[berkeman]

I think you will always have a delay in the simulation when it starts with no previous knowledge of the parameters as t=-dt. You can minimize the delay by making the step sizes smaller, obviously.

Have you tried doing this in Excel? I'd be inclined to do an Excel spreadsheet to try out ideas. Make columns for each of the quantities, with time being the left-most column.

BTW, sorry but I'm having trouble seeing what the motion is. Are you simulating the motion of the platform after the mass hits it? I'm not matching that up with the inverted parabola figure...

 

[Selroth]

I think you will always have a delay in the simulation when it starts with no previous knowledge of the parameters as t=-dt. You can minimize the delay by making the step sizes smaller, obviously.

Have you tried doing this in Excel? I'd be inclined to do an Excel spreadsheet to try out ideas. Make columns for each of the quantities, with time being the left-most column.

BTW, sorry but I'm having trouble seeing what the motion is. Are you simulating the motion of the platform after the mass hits it? I'm not matching that up with the inverted parabola figure...

Thanks for the reply!

Aye. A smaller time interval will yield more accurate results, and if the computer processed infinitely fast with an infinitely small time interval, it would be perfectly accurate. :)

I was hoping there may be some math trick to this that I'm just not seeing. Since I have the initial velocity, I can also figure it's kinetic energy, and try using energy conservation. But, the potential energy stored by the spring requires the position, which puts us back at my original problem.

I could play with excel later, and use better numbers (the numbers in my code example probably won't work well if you actually ran it). If I still have this problem, I'll probably make a smaller, simpler program (a javascript page) that runs very similar code. Can also play with excel, and do a comparison between real and simulated values. A good idea - thanks!

As for the motion, the ball drops at t0, falls, hits the platform at t6, and compresses the platform's spring thereafter. The ball /should/ return to its original height at some tX (though my current simulations fail to do this, and either have the ball pass through the spring or rocket off).

The parabola chart is the spring's force over time. It is not the ball's position.

 

[berkeman]

Thanks for the reply!

Aye. A smaller time interval will yield more accurate results, and if the computer processed infinitely fast with an infinitely small time interval, it would be perfectly accurate. :)

I was hoping there may be some math trick to this that I'm just not seeing. Since I have the initial velocity, I can also figure it's kinetic energy, and try using energy conservation. But, the potential energy stored by the spring requires the position, which puts us back at my original problem.

I could play with excel later, and use better numbers (the numbers in my code example probably won't work well if you actually ran it). If I still have this problem, I'll probably make a smaller, simpler program (a javascript page) that runs very similar code. Can also play with excel, and do a comparison between real and simulated values. A good idea - thanks!

As for the motion, the ball drops at t0, falls, hits the platform at t6, and compresses the platform's spring thereafter. The ball /should/ return to its original height at some tX (though my current simulations fail to do this, and either have the ball pass through the spring or rocket off).

The parabola chart is the spring's force over time. It is not the ball's position.

Ah, makes more sense now. The parabolic force graph would have to be for the cases that you say the ball "rockets off", though, right? The fact that the spring force decreases for the 2nd half of the parabola implies that the spring is de-compressing.

Can you post the ball's velocity and position graphs along with the force parabola? That may give some clues to where those quantities are encountering a problem...

 

[Selroth]

Ah, makes more sense now. The parabolic force graph would have to be for the cases that you say the ball "rockets off", though, right? The fact that the spring force decreases for the 2nd half of the parabola implies that the spring is de-compressing.

Can you post the ball's velocity and position graphs along with the force parabola? That may give some clues to where those quantities are encountering a problem...

Unfortunately, the graph was drawn freehand as an approximation and simply to give myself a way to visualize what's happening. I could perhaps freehand a position and velocity graph as well, but none of these graphs are meant to be to scale/reference-able.

Allow me to elaborate on how I used the graph. At t6 the ball has just touched the spring. At exactly t6, it's correct to say the force is 0. However, the program must make a leap of time over the time interval. This is where the simulated position of the ball, and the realistic position of the ball begin to take separate paths. Next comes t7. The program sees the position of the ball as if no force was ever applied to it. However, if it were real, force would have been applied to the ball between t6 and t7, thus the position would be less (potentially much less).

Additionally (and not shown in the graphs), because the position is too large, the force generated by the spring at t7 will too large.

 

[AlephZero]

To get started on a better way, forget about the times when the particle makes contact with the platform and leaves it.

What you did was to find the conditions at the start of the time step, and assume they remain constant for the whole step. That is clearly "wrong" so far as the force in the spring is concerned, as you said.

So, let's assume something differnent: the acceleration over the whole step is constant, not the force.

If the acceleration is a, at the start of the step you have
$x_0 = x_0$
and at the end
$x_t = x_0 + v_0 t + at^2/2$
$v_t = v_0 + at$
Everything is known except for a.
You can find the forces at the start and end of the step in terms of a:
$f_0 = -k x_0 + W$ where W is the weight (force due to gravity).
$f_t = -k x_t + W = -k(x_0 + v_0 t + at^2/2) + W$
Now, since a is the average accleration, let's assume it corresponds to the average force in the interval, and approximate the average force by $(f_0 + f_t)/2$
That gives
$ma = (f_0 + f_t)/2 = -k(x_0 + v_0t/2 + at^2/4) + W$

You can rearrange that equation to find a, then use a to find $x_t$ and $v_t$.
This is a standard method called the "average acceleration" method, and it's also a special case of a family of methods invented by somebody called Newmark. Google for "Newmark integration" for more.

For the steps where the ball contacts or leaves the platform, you can iterate to get a "constent" set of assumptions. For example calculate the $f_t$ assuming the ball is in contact at the end of the step, and then see if $x_t$ really is in contact. If it isn't, try the other option. If neither of them give a constistent result, you can do something empirical like take the average of the two final displacements and velocities (and reduce the time step for the simulation, if that isn't accurate enough).

 

[Selroth]

To get started on a better way, forget about the times when the particle makes contact with the platform and leaves it.

What you did was to find the conditions at the start of the time step, and assume they remain constant for the whole step. That is clearly "wrong" so far as the force in the spring is concerned, as you said.

So, let's assume something differnent: the acceleration over the whole step is constant, not the force.

If the acceleration is a, at the start of the step you have
$x_0 = x_0$
and at the end
$x_t = x_0 + v_0 t + at^2/2$
$v_t = v_0 + at$
Everything is known except for a.
You can find the forces at the start and end of the step in terms of a:
$f_0 = -k x_0 + W$ where W is the weight (force due to gravity).
$f_t = -k x_t + W = -k(x_0 + v_0 t + at^2/2) + W$
Now, since a is the average accleration, let's assume it corresponds to the average force in the interval, and approximate the average force by $(f_0 + f_t)/2$
That gives
$ma = (f_0 + f_t)/2 = -k(x_0 + v_0t/2 + at^2/4) + W$

You can rearrange that equation to find a, then use a to find $x_t$ and $v_t$.
This is a standard method called the "average acceleration" method, and it's also a special case of a family of methods invented by somebody called Newmark. Google for "Newmark integration" for more.

For the steps where the ball contacts or leaves the platform, you can iterate to get a "constent" set of assumptions. For example calculate the $f_t$ assuming the ball is in contact at the end of the step, and then see if $x_t$ really is in contact. If it isn't, try the other option. If neither of them give a constistent result, you can do something empirical like take the average of the two final displacements and velocities (and reduce the time step for the simulation, if that isn't accurate enough).

Genius! This looks very, very promising! It's a bit late for me to dig into it right now, but I look forward to implementing this tomorrow or later this week! Thank you very much AlephZero!