- #1
gracy
- 2,486
- 83
Formula for time of flight in projectile motion is 2usin theta/g but I think it is only applicable for when object is launched from ground i.e in the case below
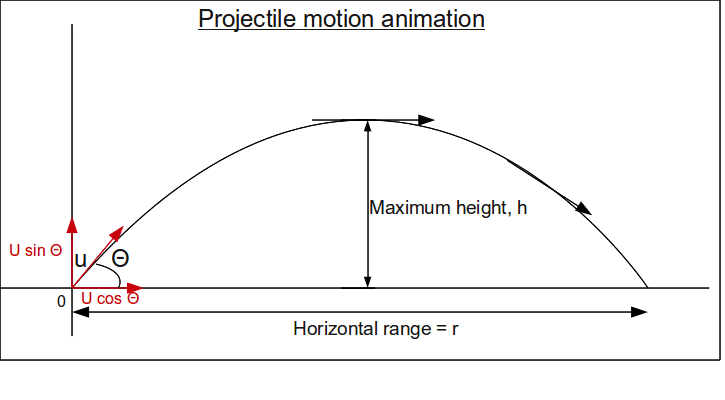
But when it is launched from certain height this formula is no longer in use.
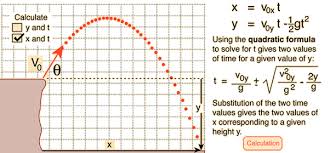
But when it is launched from certain height this formula is no longer in use.
Last edited: