Proof by induction, puzzles by answer

  • Context: Undergrad 
  • Thread starter Thread starter MegaDeth
  • Start date Start date
  • Tags Tags
    Induction Proof
Click For Summary

Discussion Overview

The discussion revolves around a proof by induction question, specifically focusing on the transition from the expression 2^(k+1) to 2^(k+2). Participants are seeking clarification on the mathematical steps involved in this transformation.

Discussion Character

  • Technical explanation

Main Points Raised

  • One participant expresses confusion about the transition from 2^(k+1) to 2^(k+2) and requests clarification.
  • Another participant suggests that more background information is needed to address the question effectively.
  • A third participant notes that an image linked in the discussion did not load properly, hindering the ability to respond accurately.
  • A later reply attempts to clarify the transformation by stating that multiplying 2^(k+1) by 2 results in 2^(k+2), explaining that this is due to raising the exponent by 1.
  • Another participant reiterates the multiplication of 2^(k+1) by 2, confirming the resulting expression as 2^(k+2).

Areas of Agreement / Disagreement

The discussion shows some participants agreeing on the mathematical reasoning behind the transformation, while others express confusion and seek further clarification. No consensus is reached on the overall understanding of the proof.

Contextual Notes

Participants have not provided sufficient background or context regarding the specific proof by induction being discussed, which may limit understanding. Additionally, the lack of a properly linked image may contribute to the confusion.

MegaDeth
Messages
83
Reaction score
0
Ok, so there's this proof by induction question. I looked at the answer for it but I don't understand it.

TuXle.jpg


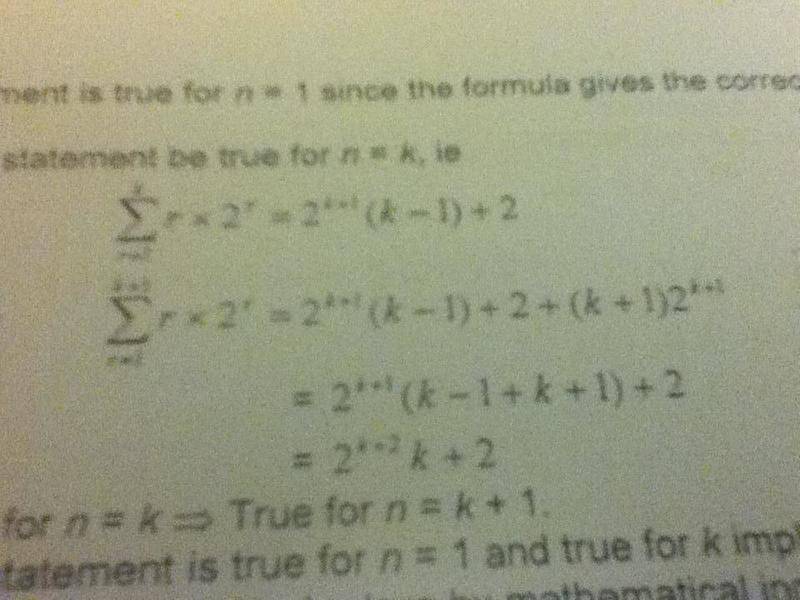
How does it get from being 2^(k+1) to being 2^(k+2)?
 
Last edited by a moderator:
Physics news on Phys.org
You need to provide a little more background into your question, I think.
 
Your image did not link properly so it is impossible to answer your question.
 
MegaDeth said:
How does it get from being 2^(k+1) to being 2^(k+2)?
2^{k+1}(k-1+k+1) = 2^{k+1}(2k) = 2^{k+2}k
 
you got [2^(k+1)](2k).

multiply 2^(k+1) by two, that is raising your exponent by 1. Hence 2^(k+2)
 
Last edited:

Similar threads

Undergrad Spivak, Ch. 20: Understanding a step in the proof of lemma
  • · Replies 1 ·
Replies
1
Views
3K
High School Why do I not understand what seems to be basic Calculus?
  • · Replies 11 ·
Replies
11
Views
3K
Undergrad Use of induction in the proof of the Chinese Remainder Theorem
  • · Replies 7 ·
Replies
7
Views
3K
Undergrad Proof by induction of block diagonal decomposition of a matrix
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Is there any way to simplify my proof by induction?
  • · Replies 13 ·
Replies
13
Views
2K
Undergrad Explicit logical justification for last step in epsilon/delta proof?
  • · Replies 20 ·
Replies
20
Views
2K
Do these two statements imply an underlying induction proof?
  • · Replies 7 ·
Replies
7
Views
1K
Undergrad How do I use induction more rigorously when making Taylor expansions?
  • · Replies 7 ·
Replies
7
Views
2K
Undergrad Looking for Guarantees that the method of fixed-point iteration will work
  • · Replies 22 ·
Replies
22
Views
3K
Prove that ##5 | (2^n a) \rightarrow (5 | a)##for any ##n##
  • · Replies 10 ·
Replies
10
Views
3K