View attachment 2541
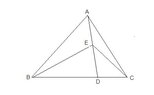
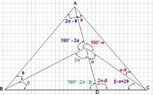
Since AB=AC, I first let $\angle CED=\alpha$, then $\angle EBC=\beta$ and $\angle DAC=\theta$.
A little working on the triangle $EBC$ shows that $\alpha+\beta+\theta=90^{\circ}$
Consider the triangles $EBD$ and $ECD$, we have:
$\dfrac{ED}{\sin \beta}=\dfrac{BD}{\sin 2\alpha}$ and $\dfrac{ED}{\sin(\beta-\alpha+2\theta)}=\dfrac{CD}{\sin \alpha}$
This yields
$\dfrac{BD}{CD}=\left(\dfrac{\sin 2\alpha}{\sin \alpha} \right)\left(\dfrac{\sin (\beta-\alpha+2\theta)}{\sin \beta} \right)$
We then try to eliminate the variable $\beta$ by using the relation $\beta=90^{\circ}-(\alpha+\theta)$, we get:
$\begin{align*}\dfrac{BD}{CD}&=\left(\dfrac{\sin 2\alpha}{\sin \alpha} \right) \left(\dfrac{\sin (90^{\circ}-(\theta+\alpha))-\alpha+2\theta)}{\sin (90^{\circ}-(\theta+\alpha))} \right)\\&=\dfrac{\sin 2\alpha}{\sin \alpha}\cdot\dfrac{\sin (90^{\circ}-(2\alpha-\theta))}{\sin(90^{\circ}-(\theta+\alpha))}\\&=\dfrac{\sin 2\alpha}{\sin \alpha}\cdot\dfrac{\cos (2\alpha-\theta)}{\cos (\theta+\alpha)}\\&=\dfrac{\sin 2\alpha}{\sin \alpha}\cdot\dfrac{\cos 2\alpha \cos\theta+\sin 2\alpha \sin \theta}{\cos \theta \cos\alpha-\sin \theta \sin \alpha}(*)\end{align*}$
We know the RHS expression will be reduced to 2, so, I think eliminating another variable would be a wise way to go.
Now, consider the triangles $ABE$ and $ACE$, we have:
$\dfrac{AB}{\sin(180^{\circ}- 2\alpha)}=\dfrac{AE}{\sin \theta}$ and $\dfrac{AC}{\sin(180^{\circ}- \alpha)}=\dfrac{AE}{\sin(\alpha-\theta)}$
Since $AB=AC$, the above simplifies to:
$\dfrac{\sin 2\alpha}{\sin \theta}=\dfrac{\sin \alpha}{\sin(\alpha-\theta)}$
$\dfrac{2\sin \alpha \cos \alpha}{\sin \alpha}\cdot\sin(\alpha-\theta)=\sin \theta$
$2\cos \alpha\cdot\sin(\alpha-\theta)=\sin \theta$
$2\cos \alpha\cdot(\sin \alpha \cos\theta-\cos \alpha \sin\theta)=\sin \theta$
$2\cos \alpha\cdot\sin \alpha \cos\theta=\sin \theta(1+2\cos ^2 \alpha)$
$\tan \theta=\dfrac{\sin 2\alpha}{1+2\cos ^2 \alpha}$ (**)
To merge these two equations ((**)and (*)), we divide the equation (*), top and bottom, by $\cos \theta$ to get:
$\dfrac{BD}{CD}=\dfrac{\sin 2\alpha}{\sin \alpha}\cdot \dfrac{\cos 2\alpha +\sin 2\alpha \tan\theta}{\cos \alpha -\sin \alpha \tan\theta}$
therefore,
$\begin{align*}\dfrac{BD}{CD}&=\dfrac{2\sin \alpha \cos \alpha}{\sin \alpha}\cdot \dfrac{\cos 2\alpha +\sin 2\alpha\cdot\frac{\sin 2\alpha}{1+2\cos ^2 \alpha}}{\cos \alpha-\sin \alpha\left(\dfrac{\sin 2\alpha}{1+2\cos ^2 \alpha} \right)}\\&=2 \cos \alpha\cdot \dfrac{\cos 2\alpha +2\cos^2 \alpha \cos 2\alpha+\sin^2 2\alpha}{\cos \alpha+2\cos^3 \alpha-\sin \alpha \sin 2\alpha}\\&=2 \cos \alpha\cdot \dfrac{\cos 2\alpha(1+2\cos^2 \alpha)+\sin^2 2\alpha}{\cos \alpha+2\cos^3 \alpha-2\sin \alpha \sin \alpha \cos \alpha}\\&=2 \cos \alpha\cdot \dfrac{\cos 2\alpha(\cos 2\alpha+2)+\sin^2 2\alpha}{\cos \alpha(1+2\cos^2\alpha-2\sin^2 \alpha)}\\&=2 \cos \alpha\cdot \dfrac{\cos^2 2\alpha+\sin^2 2\alpha+2\cos 2\alpha}{\cos \alpha(1+2(\cos^2\alpha-\sin^2 \alpha))}\\&=2 \cos \alpha\cdot \dfrac{1+2\cos 2\alpha}{\cos \alpha(1+2\cos 2\alpha)}\\&=2 \cos \alpha\cdot\dfrac{1}{\cos \alpha}\\&=2 \end{align*}$
Hence,
$BD=2CD$ (Q.E.D.)